|
|
|
|
|
|
|
|

|
Disclaimer Copyright © Intel Corporation (1996). Third-party brands and names are the property of their respective owners.
|
Summary
This application note presents an optimized MMX(TM) technology
texture mapping algorithm, using bilinear interpolation as a filter and
quadratic approximation for perspective correction. Background and a brief
description appear in sections 1 and 2. Sections 2-4 describes the flow
of the code. Peformance analysis is given in section 6, proving the MMX
code about 5x faster than optimized C code. Complete inner-loop source
code is given in the Appendices, but the user will need to create an application
around this inner loop. Note that bilinear interpolation is a high-quality
data-intensive algorithm; simpler methods like linear interpolation or
point-sampling will yield higher pixel rates but lower quality.
1.0 Introduction
The Intel Architecture MMX(TM) technology extensions use a Single
Instruction Multiple Data (SIMD) technique to speed up software, by processing
multiple data elements in parallel. This application note illustrates how
to use the SIMD techniques to achieve better performance in filtered 3D
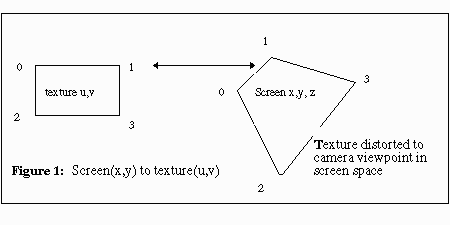
graphics texture mapping. Texture mapping is a process of assigning a texture
bitmap coordinate to a screen coordinate as shown in Figure 1.
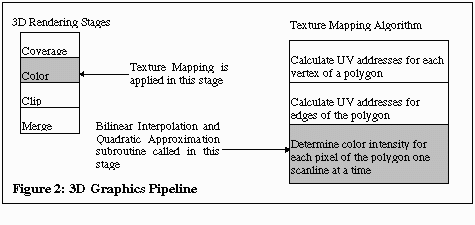
This code does perspective texture mapping with Bilinear Interpolation for filtering and Quadratic Approximation for perspective correction. Figure 2 shows where the algorithm fits in a typical 3D rendering engine.
2.0 The
Bilinear Interpolation Algorithm
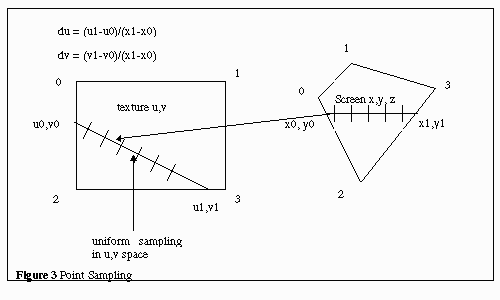
Bilinear interpolation is a filter for texture mapping. Texture mapping
based on a simple “point sampling” algorithm samples one texture coordinate
for each pixel coordinate, as shown in Figure 3. But that can yield very
“blocky” or “pixellated” results, especially when the texture is seen close
up (magnified) on the screen. For smoother appearance, bilinear interpolation
samples 4 texture pixels, taking a weighted average to produce each pixel
on the screen.
Given a screen pixel point and a texel coordinate (U.u,V.v), the algorithm finds 4 adjacent points on the texture map and interpolates the RGB color intensity for the pixel based on the colors of the 4 points. The RGB color intensity is calculated by multiplying the four points by a weighting factor(equations 1-4) and adding the results, as shown in Figure 4.
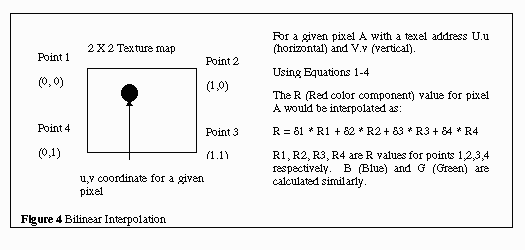
The algorithm is given a U.u,V.v coordinate, which contains a integer part and a fractional part. The integer part is extracted to obtain the first point in the texture, (U, V). The 3 adjacent points are (U+1, V), (U,V+1), (U+1, V+1). The actual (U.u,V.v) point is located somewhere within these 4 points. The RGB values of each of these four points are read, and the RGB value for the corresponding pixel is interpolated from these four points and the fractional parts.
The fractional part of the U.u,V.v coordinate is used to calculate the
weight factor for each of the 4 points. Let the fractional part of U.u
be .u and the fractional part of V.v be .v. Let (U, V), (U+1), (U+1, V+1)
and (U, V+1) be point1, point2, point3, and point4 respectively, and let
ð1, ð2, ð3 and ð4 the weight factor for points 1 through
4 respectively. Then the equations for the four factors are given below:
ð1 = (1- .u) · (1 - .v)
(1)
ð2 = .u · (1 - .v)
(2)
ð3 = .u · .v
(3)
ð4 = (1 - .u) · .v
(4)
The new RGB value for the pixel being mapped is given by the equations
below:
R = R1 · ð1 + R2 · ð2 + R3 · ð3 + R4 · ð4
(5)
G = G1 · ð1 + G2 · ð2 + G3 · ð3 + G4 · ð4
(6)
B = B1 · ð1 + B2 · ð2 + B3 · ð3 + B4 · ð4
(7)
where Rx, Gx and Bx are RGB values for point x, where x can be 1, 2,
3, and 4.
2.1
Quadratic Approximation Algorithm
Quadratic Approximation is used in perspective texture mapping
to eliminate distortions in mapped images. For a scanline, the first u,v
point is given and the du, dv, ddu, ddv values are given to calculate the
next u,v point. The du and dv parameters are texture slopes, and they determine
how UV addresses change from one pixel to the next. ddu and ddv are the
slopes of du and dv. The height and length of a 3D object become compressed(appear
shorter) as it goes away from the viewer. The UV address will be changed
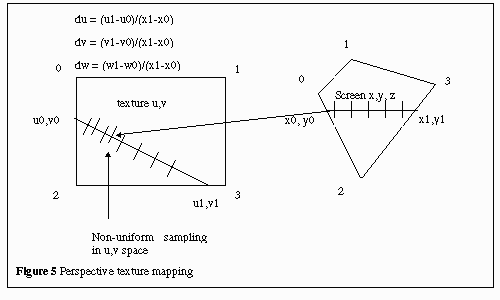
in larger steps as the polygons move away from the viewer. For true perspective
correction of the texture, two divisions by W are needed for each pixel
as shown in Figure 5. (W is the world space coefficient, derived from the
4x4 matrices used to transform each vertex from its location in its local
“model” space to the camera viewpoint in screen space). Quadratic approximation
is used to approximate the “1/W” effect, avoiding the division operations.
By quadratic approximation, we mean addition of a delta to U & V at
each screen horizontal scanline step, and addition of a second-order differential
to the delta factors.
The second-order differentials, ddu and ddv, approximate the 1/W division.
This algorithm is given by the equations below:
ui+1 = ui + dui
(8)
vi+1 = vi + dvi
(9)
dui+1 = dui + ddu
(10)
dvi+1 = dvi + ddv
(11)
For background information on calculating the quadratic values ddu and
ddv, and their derivation from 1/W, refer to "Digital Image Warping"
by George Wolberg, pg. 297 Appendix 3.[ IEEE Computer Society Press, July
1990. ISBN 0-8186-8944-7]
3.0 Input and Output Data Representation
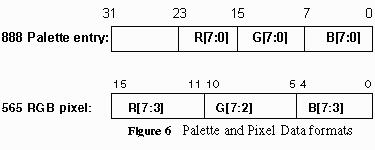
The intensity of a pixel is represented by a 16-bit WORD in which the RGB is stored in a 565 data format: 5 bits for R, 6 bits for G and 5 bits for B. However, the algorithm can be easily modified for 555 color format. The color of a texel is represented by a byte unsigned number. The byte is an index to the color palette entry, where the actual color intensity is stored. Each color palette is represented by a 32-bit DWORD, in which the RGB values, are stored in the lowest 24 bits. A 24-bit color palette is used instead of 565 RGB format because color calculation is done in bytes or words. The (U.u,V.v) coordinates of a texture map are represented by 32-bit DWORD, in which the value is a 16.16 number(16 bit integer part and 16 bit fractional part). The du, dv, ddu, and ddv values also share the same data format. Refer to Figure 6 and 7 for further clarification.
The ranges of R,G and B values and the color palette index are from
0 to 255. The 16 bit fractional part of the u,v values will be truncated
to 15 bit for signed multiplication. The texture map must be square, with
each side 0 <= u, v < 2N, where 2N is the size
of the texture. U and V must be values between 0 and 255.
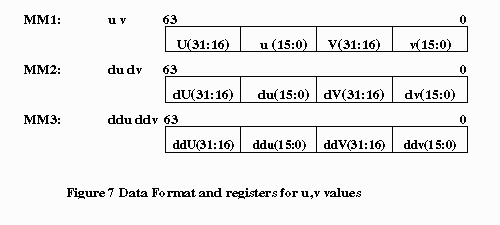
Each value is a 16.16 DWORD, with U & V unsigned, and du, ddu, dv,
and ddv signed.
4.0 Code Partitioning
The procedure is composed of two sections: data setup, and inner
loop. The data setup section copies the data pointers to the general purpose
registers and copies the u,v, du,dv,ddu and ddv values to the MMX registers.
The inner loop section consists of setting up data for parallel multiplication
and addition, manipulating the integer and fractional part of the (u,v)
coordinate, calculating the corresponding pixel intensity, and writing
the result to memory.
4.1 Data Setup
There are three tasks in data setup: move texel map pointer
and palette pointer to EAX and ECX respectively, and unpack u, v, du, dv,
ddu and ddv values to MM1, MM2 and MM3 respectively. Five unpack instructions
are used to arrange the data.
4.2 Inner Loop Section
The inner loop performs the bulk of the bilinear interpolation
and quadratic approximation. There are 6 major tasks: Calculating the 4
ð multipliers, calculating the integer (U.u,V.v) which references the
linear memory array of the texture map, reading the 4 palette indices (texels)
and corresponding RGB pixels from the palette, arranging them in the proper
format, calculating the new RGB intensity for the screen pixel, and finally
calculating the next (U.u,V.v) point.
4.2.1
Calculating the 4 ð multipliers
This is the most challenging part of the code in terms of the
number of instructions required. First there are accuracy versus instruction
count issues. The algorithm requires calculating (1 - .u) and (1 - .v),
which is the same as taking the 2’s complement of both values. However,
if .u or .v were 0, the code needs to produce a result of 1. The multipliers,
however, are fractional fixed point values. In order to handle this special
case, there would be added instructions and conditional statements. Taking
the 1’s complement of .u and .v to approximate (1 - .u) and (1 - .v) is
the better solution; although it will lose one bit of accuracy. In cases
where .u and .v equals 0 or 0.5, the final result is accurate to within
one lsbit. This is tolerable since the fractional part is truncated to
16 bits anyway, and the algorithm only uses the integer part of the result.
Due to the way the pixels are read into the registers, the ð multipliers
are arranged in the format shown below:
MM1: ð4 ð1 ð4 ð1
MM2: ð2 ð3 ð2 ð3
MM3: ð4 ð1 ð2 ð3
This arrangement is used to speed up the RGB color calculation. pmulhw is used to obtain the high word as the final result. Figure 8 below illustrates the code. NOTE: the example code below is not optimized for pairing, but for ease of reading; however, the full code listings in the appendices are optimized.
.DATA
reg_clr5 DWORD 0000ffffh, 0000ffffh
reg_xoru1 DWORD 7fff7fffh, 7fff7fffh
reg_xorv1 DWORD 00007fffh, 00007fffh
reg_xorv2 DWORD 7fff0000h, 7fff0000h
.code
pand mm0, reg_clr5
; clear out integer part
psrld mm0, 1
; shift u,v 1 bit for sign multiply
movq mm4, mm0
; make a copy for the other operand
punpcklwd mm0, mm0
; mm0 = - - u u
punpckhwd mm4, mm4
; mm4 = - - v v
punpckldq mm0, mm0
; mm0 = u u u u
punpckldq mm4, mm4
; mm4 = v v v v
movq mm3, mm4
; mm3 = v v v v
pxor mm4, reg_xorv2
; 1's complement mm4 = ~v v ~v v
pmulhw mm4, mm0
; mm4 = ð2 ð3 ð2 ð3
movq mm7, mm4
; mm7 = ð2 ð3 ð2 ð3
pxor mm3, reg_xorv1
; 1's complement mm3 = v ~v v ~v
pxor mm0, reg_xoru1
; mm0 = ~u ~u ~u ~u
pmulhw mm3, mm0
; mm3 = ð4 ð1 ð4 ð1
punpckldq mm4, mm3
; mm4 = ð4 ð1 ð2 ð3
Figure 8: Implementation of ð multiplier
4.2.2
Calculating the Integer Part of U,V
This section explains the steps in calculating the integer part
of the (U.u,V.v) coordinate. (U, V) is used to reference the palettized
8-bit texel stored in the texture map. The texture map is a 256X256 array
(or 64K linear memory segment), where each entry is 8 bits wide. Hence,
the displacement in the texture map for a given (U, V) coordinate is U+V*256.
This references point 1 in the texture map. Let’s call this point pt1.
(If the texture map were instead 16 or 24 bits/pixel, then the V-multiplier
would need to be scaled accordingly by another factor of 2 or 3.)
Point 2 in the texture map is then pt1 + 1, point 3 is pt1 + 256 and point
4 is pt1 + 257. There is also one special case to consider when the 3 adjacent
points go out of the 256 X 256 frame. This implementation uses tiling to
solve this problem. Tiling simply wraps the number around when any of the
points go out of the 256 X 256 frame. For example, a point with u= 256
and v=256 is the same as a point with u=0 and v=0. This code is given in
Figure 9.
An alternative to tiling is to wrap-around to the next texture scanline
when at the right edge of the texture. However, it reduces quality and
it only saves 4 instructions, or 2 cycles when paired, for the 256x256
texture-size hardwired case.
The texels are read in the following order: pt1, pt4, pt3, pt2. This particular
order is chosen to minimize the number of instructions required to calculate
the pointers to the four texel points.
.DATA
reg_clr6 DWORD 00ffh, 00ffh
; calculate index in linear texel map array based on U & V
psrld mm7, 16
; get integer part of U.u and V.v
pand mm7, reg_clr6
; allow only 256x256 texture size
movq mm6, mm7
; mm6 = mm7 = 0 V 0 U (integer part)
psrlq mm6, 24
; mm6 = 0 0 0 [V*256](shifted 24=32-8places)
paddd mm6, mm7
; mm6 = 0 V 0 [U+V*256]
movd eax, mm6
; move index to eax to get point 1
mov ebx, eax
; copy index value
; read in texel and color one texel at a time
xor edx, edx
; used to prevent Pentium Pro processor stalls
mov dl, [esi][eax]
; get color pallette pointer of
point 1movq mm5, [edi][edx*4]
; get RGB of point 1 from color
pallete; mm5 = - - - - 0 R1 G1 B1
add eax, 256
; calculate point 4 index
and eax, 0ffffh
; take modulo 256x256
xor edx, edx
;
mov dl, [esi][eax]
; get color pallette index of
point 4punpcklbw mm5, [edi][edx*4]
; get RGB of point 4 from color
pallete; mm5 = 0 0 R4 R1 G4 G1 B4 B1
add ebx, 1
; calculate point 3 index
and ebx, 0ffh
; take modulo 256
and eax, 0ff00h
; retain only y component
or eax, ebx
; linear address calculation
xor edx, edx
;
mov dl, [esi][eax]
; get color pallete index of point 3
movq mm6, [edi][edx*4]
; get RGB of point 3 from color
pallete; mm6 = - - - - 0 R3 G3 B3
add eax, 0ff00h
; calculate point 2 index
and eax, 0ffffh
; take modulo 256x256
xor edx, edx
;
mov dl, [esi][eax]
; get color pallete index of point 2
punpcklbw mm6, [edi][edx*4]
; get RGB of point 2 from color
pallete; mm6 = 0 0 R2 R3 G2 G3 B2 B3
Figure 9: Texture map displacement calculation
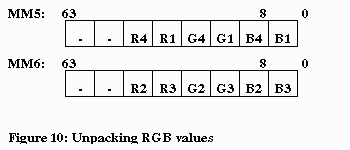
4.2.3 Reading Four RGB intensity values
Code for reading color values is intermixed with the (U,V) coordinate
calculations (Figure 9). Each texel is read immediately after the texel
address is known. Two 24-bit texels are packed into one MMX register as
each is read from the palette (Figure 10). This arrangement facilitates
parallel PMADD instructions, as explained in the next section, and reduces
the number of registers to temporarily store these values.
4.2.4
Calculating the RGB intensity for the pixel
This part calculates the final texel result to write to the
output buffer. The ð multipliers are stored in available MMX registers
in the format as discussed in section 4.2.1. Figure 11 illustrates the
flow of the data.
The code for the calculation is given in Figure 12. The MMX registers used
here are different from the actual code for the sake of clarification.
Because of the way the RGB values are arranged, we are able to perform
multiply and add on two pixels in parallel.
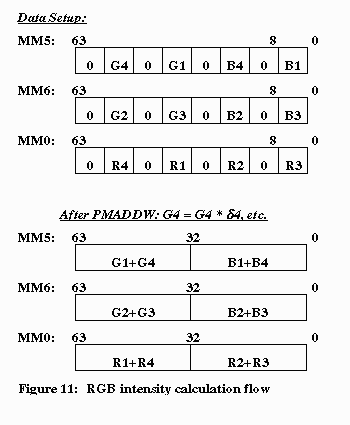
The “R” is calculated by further unpacking MM0 and using one more addition.
The final “G” and “B” value are calculated with just one more addition
by adding MM5 and MM6. The final RGB format can be obtained using “shift”
and “or” instructions.
; arrange RGB values in proper format for parallel multiply
xor mm7, mm7
; mm7 = 0 0 0 0
movq mm3, mm5
; mm3 = mm5 = 0 0 R4 R1 G4 G1 B4 B1
punpcklbw mm5, mm7
; mm5 = 0 G4 0 G1 0 B4 0 B1
movq mm0, mm6
; mm0 = mm6 = 0 0 R2 R3 G2 G3 B2 B3
punpcklbw mm6, mm7
; mm6 = 0 G2 0 G3 0 B2 0 B3
punpckhwd mm0, mm3
; mm0 = 0 0 0 0 R4 R1 R2 R3
punpcklbw mm0, mm7
; mm0 = 0 R4 0 R1 0 R2 0 R3
pmaddwd mm5, mm1
; mm5 = G41 B41 -- mm1 = ð4 ð1 ð4 ð1
pmaddwd mm6, mm2
; mm6 = G23 B23 -- mm2 = ð2 ð3 ð2 ð3
pmaddwd mm0, mm3
; mm0 = R41 R23 -- mm3 = ð4 ð1 ð2 ð3
punpckldq mm4, mm0
; mm4 = R23 -
paddd mm5, mm6
; mm5 = G B
paddd mm0, mm4
; mm0 = R -
Figure 12: RGB intensity calculation
The final required data format as required by different video cards
or software can be easily obtained with a few more MMX instructions. This
code implements the 565 format as shown in Figure 6 and Figure 13 below.
But 555 or 24(888) bit color can also be easily obtained, with 24 bit color
requiring the fewest instructions.
; converts 24 bit color to 16 bit color
pand mm5, reg_clr2
; clear out irrelevant bits(G and B)
; 2 relevant bits are in lower word
; due to ð multipliers shifted by 2 bits
pand mm0, reg_clr3
; clear out irrelevant bits(Red)
punpckhdq mm7, mm5
; mm7 = G -
psrld mm5, 17
; B is correct position
psrlq mm7, 43
; G is correct position
por mm5, mm7
; B with G
psrlq mm0, 38
; R in correct position
por mm5, mm0
; final result in mm5: 565 RGB format
Figure 13: 565 data format manipulation
4.2.6
Quadratic Approximation implementation
This implementation requires only 2 lines of code in the inner
loop.
paddd mm1, mm2
; performs u = u + du, v = v + dv
paddd mm2, mm3
; performs du1 = du0 + ddu and
dv1 = dv0 + ddvFigure 14: Quadratic Approximation Implementation
There are three different versions of the texture mapping code:
1: Optimized with MMX
technology. It supports only 256X256 texture size.
2: Scalar C version, for
performance comparison and functional description. NOTE THAT this C code
is NOT OPTIMIZED.
3: A more flexible implementation
with MMX technology. Allows user-specified texture sizes: 16x16, 32x32,
64x64, 128x128, or 256x256. Two more input parameters are required for
this version. Because of the added instructions, the third version requires
4 more cycles.
All three versions of the code are given in the appendices.
6.0 Tradeoffs
There were three major design issues made to optimize for performance.
Additional instructions were added to eliminate partial stalls on the Pentium(R)
Pro processor. Accuracy was compromised for speed. Loop unrolling was not
used, thus avoiding added complexity and more instructions.
XOR instructions are added to eliminate “partial-stalls” on the Pentium
Pro processor, as shown in Figure 9. On that processor, accesses to a 32-bit
register(EAX, EBX, ECX, EDX, etc...) after some previous instruction wrote
to a partial register(AL, AH, AX, etc...) causes a partial-stall penalty
of more than 6 clocks (the execution stops until the 16-bit or 8-bit partial-register
update completes). By adding an XOR instruction “XOR EAX, EAX”, as recommended
by VTune 2.0, the partial-stall caused by a byte update of AL is avoided.
This added a total of 4 instructions in the inner loop, but it saved 24
penalty cycles.
As described earlier, a 1’s complement was used to approximate two’s complement
(1- .x) numbers. Although one digit of accuracy is lost, it saves 2-4 instructions
per subtraction.
There is one 16-bit write per iteration, of the RGB value to the screen.
It would be possible to unroll the loop 4 times to take advantage the movq
instruction to store 8 bytes to memory each time. However, the overhead
might actually slow down the code. To implement loop unrolling, we have
to consider the variations in the number of pixels per scanline. This requires
conditional statements, which can cause branch mispredictions due to the
irregularity of the pixel counts in a scanline. Note that the Pentium(R)
Pro processor stalls 12 cycles for a branch mispredict
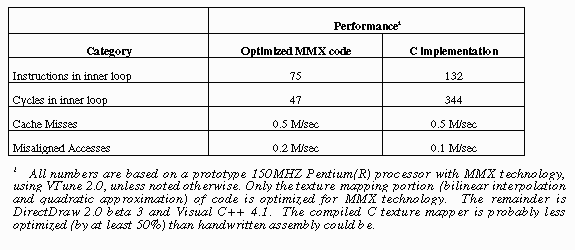
7.0 Performance
The optimized code has 103 instructions. With pairing, it requires
73 cycles to execute assuming an infinite cache. The inner loop requires
47 cycles. With a 16K L1 data cache, the frequency of cache hit per scanline
depends on how the du, dv, ddu, and ddv vary and on the size of texture
map. For example, du=1, dv=0 will sequentially fetch texels from a single
cache line, with very good performance; but du>31 and/or dv>0 will
skip across multiple cache lines at each texel fetch. Large (such as 256x256
byte = 64kB total) textures will have poorer L1 cache hit ratios than smaller
textures(such as 32x32 = 1kB).
The number of pixels per scanline determines how many times the inner loop
executes. The inner loop has four byte-sized reads (8-bit texture map entries)
and four DWORD reads (color palette). The regularity in locality of reference
of the texture map depends on the geometry and orientation of the rendered
object. The four references to the color palette do not have any locality.
However, since the color palette has only 256 entries of four bytes each,
the entire palette has a good chance of being in the cache most of the
time.
The table below gives lists the number of clocks required to map a given
a scanline based on the number of pixels per scanline. Note that clock
counts increase linearly with the number of pixels, due to the small overhead
required per scanline. A total of 16 clocks are required in the outer loop,
independent of the pixel count per scanline.
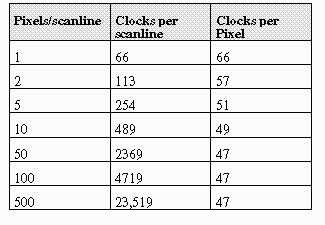
Please reference the Table below for a comparison and performance analysis
of the MMX technology and scalar implementation of texture mapping using
bilinear interpolation and quadratic approximation. By commenting out the
updates of ddu and ddv in the code, the reader can determine the (miniscule)
performance impact and (significant) quality impact of non-perspective-correct
mapping.
The executables for the two applications were compiled with Microsoft Visual
C++ 4.1, with speed optimization turned on. Timings were measured with
Intel’s VTune 2.0. [see http://www.intel.com/ial/vtune for information
on ordering this product.]
We leave as an excercise for the reader, the following worthwhile activities:
· Adaptation to RGB24 and/or RGB555 output pixel formats.
· Adaptation to RGB24 and/or RGB555 or RGB565 textures (no
palette).
· Transparent, blended, or chromakeyed textures
· Shaded and lit textures
· Fog
9.0 Tidbits
Below is a list of tips learned from writing this code:
· Reduce the number of pack and unpack instructions where
possible. Shift and pack instructions share one shifter, so they can’t
be paired.
· Given two instructions that are pairable(one of the instruction
can be issued to the V-pipe and the other can only be issued to the
U-pipe), schedule the one that requires the U-pipe first. Since the first
instruction is always issued to the U-pipe first on the
Pentium processor, the second instruction can’t be paired if it requires
the U-pipe.
· PMADD and PMUL each require 3 cycles. Schedule these instructions
3 cycles ahead before you reference the result.
· The data in an integer register must be ready two cycles
before it is used by an MMX instruction as an address to reference memory.
· Try to reuse MMX registers, since there are only eight.
APPENDIX A: Optimized
MMX(TM) Code
The following is the optimized MMX code that implements Bilinear
Interpolation with Quadratic Approximation for perspective correction.
It assumes a fixed 256X256 texture. Note that “NOP” instructions are inserted
to guranteed appropriate pairing in subseqent instructions. NOPs do not
add more cycles, since they are paired with other instructions.
TITLE bilquad
; prevent listing of iammx.inc file
.nolist
INCLUDE iammx.inc ; MMX technology assembly Macros
.486P
.model FLAT
;****************************************************************************
; Data Segment Declarations
;****************************************************************************
.DATA
reg_clr2 DWORD 003e0000h,
003f0000h
reg_clr3 DWORD 00000000h,
003e0000h
reg_clr4 DWORD 0000fc00h,
0f800f800h
reg_clr5 DWORD 0000ffffh,
0000ffffh
reg_clr6 DWORD 000000ffh, 000000ffh
reg_xoru1 DWORD 7fff7fffh,
7fff7fffh
reg_xorv1 DWORD 00007fffh,
00007fffh
reg_xorv2 DWORD 7fff0000h,
7fff0000h
reg_dduv DWORD 00000000h,
00000000h
reg_blnk DWORD 0h,
0h
;****************************************************************************
; Constant Segment Declarations
;****************************************************************************
.const
;****************************************************************************
; Code Segment Declarations
;****************************************************************************
.code
COMMENT ^
void bilinear_quadratic (
int32 *texel_ptr,
int32 *dest_ptr,
int32 *color_pal,
int32 num_of_pixels,
int32 u,v,du,dv,ddu,ddu);
^
bilinear_quadratic PROC NEAR C USES edi esi ebx,
texel_ptr:PTR
SDWORD, dest_ptr:PTR SDWORD,
color_pal:PTR
SDWORD,
num_of_pixels:DWORD,
u:DWORD,
v:DWORD,
du:DWORD, dv:DWORD,
ddu:DWORD,
ddv:DWORD
; move commonly used pointers to registers/initialization
movq mm1, u
; copy v coordinate to mmx register
punpckldq mm1, v
; copy u/v in mm1 register (64 bits)
movq mm2, du
; copy dv value to mmx register
movq mm7, mm1
; copy u/v for int. part conversion
punpckldq mm2, dv
; copy du/dv into one mmx register
movq mm3, ddu
; copy ddv value to mmx register
psrld mm7, 16
; get integer part of u and v
punpckldq mm3, ddv
; copy ddu/ddv to one mmx register
movq mm6, mm7
; mm6 = mm7 = 0 v 0 u (int. part)
mov ecx, dest_ptr
; move image pointer to ecx
psrlq mm6, 24
; multiply u and v by 256
movq reg_dduv, mm3
; reg_dduv = ddv ddu
paddd mm6, mm7
; mm6 = 0 [u+v*256]
mov esi, texel_ptr
; move texture image pointer to reg.
movd eax, mm6
; copy index to get point 1 Note mm6 is free
movq mm0, mm1
; make another copy of u/v for mod.
mov edi, color_pal
; move color palette base pointer to register
mov ebx, eax
; copy index value
paddd mm1, mm2
; performs u = u + du and v = v + dv
add eax, 256
; calculate point 4 index
paddd mm2, reg_dduv
; performs du1= du0 + ddu, dv = dv0 + ddv
and eax, 0ffffh
; take modulo 256x256 for point 4
biquad:
xor edx, edx
;
movq mm3, mm1
; copy u and v for integer part conversion
mov dl, [esi][ebx]
; get color pallette pointer of point 1
psrld mm3, 16
; get integer part of u and v
pand mm0, reg_clr5
; clear out integer part
pand mm3, reg_clr6
; allow only 256x256 texture size
add ebx, 1
; calculate point 3 index
and ebx, 0ffh
; prepare to add for point 3
psrld mm0, 1
; shift u,v 1 bit for sign multiply
movq mm5, [edi][edx*4]
; get RGB of point 1 from color palette
movq mm4, mm0
; make a copy for the other operand
xor edx, edx
; avoid partial stalls
punpcklwd mm0, mm0
; mm0 = - - u u
mov dl, [esi][eax]
; get color pallette index of point 4
movq mm7, mm3
; mm7 = mm3 = 0 v 0 u (integer part)
and eax, 0ff00h
; retain only y component for point 3
psrlq mm7, 24
; multiply v by 256
punpcklbw mm5, [edi][edx*4]
; get RGB of point 4 from color pallete
; mm5 = 0 0 R4 R1 G4 G1 B4 B1
add eax, ebx
; linear address calculation for point 3
xor edx, edx
; avoid partial stalls
paddd mm7, mm3
; mm7 = 0 [u+v*256] (NOTE: mm3 is free)
mov dl, [esi][eax]
; get color pallete index of point 3
punpckhwd mm4, mm4
; mm4 = - - v v
movd ebx, mm7
; move index to eax to get point 1
movq mm3, mm5
; mm3 = mm5 = 0 0 R4 R1 G4 G1 B4 B1
movq mm6, [edi][edx*4]
; get RGB of point 3 from color pallete
punpckldq mm0, mm0
; mm0= u u u u
add eax, 0ff00h
; calculate point 2 index
punpckldq mm4, mm4
; mm4 = v v v v
punpcklbw mm5, reg_blnk
; mm5 = 0 G4 0 G1 0 B4 0 B1
movq mm7, mm4
; mm7 = v v v v
pxor mm4, reg_xorv2
; 1's complement mm4 = ~v v ~v v
pxor mm7, reg_xorv1
; 1's complement mm7 = v ~v v ~v
pmulhw mm4, mm0
; mm4 = 2 3 2 3
and eax, 0ffffh
; take modulo 256x256 for point 2
NOP
pxor mm0, reg_xoru1
; mm0 = ~u ~u ~u ~u
xor edx, edx
;
mov dl, [esi][eax]
; get color pallete index of point 2
pmulhw mm7, mm0
; mm7 = 4 1 4 1
mov eax, ebx
; copy index value
NOP
punpcklbw mm6, [edi][edx*4]
; get RGB of point 2 from color pallete
; mm6 = 0 0 R2 R3 G2 G3 B2 B3
add eax, 256
; calculate point 4 index
NOP
pmaddwd mm5, mm7
; mm5 = G41 B41
movq mm0, mm6
; mm0 = mm6 = 0 0 R2 R3 G2 G3 B2 B3
punpcklbw mm6, reg_blnk
; mm6 = 0 G2 0 G3 0 B2 0 B3
punpckhwd mm0, mm3
; mm0 = 0 0 0 0 R4 R1 R2 R3
punpcklbw mm0, reg_blnk
; mm0 = 0 R4 0 R1 0 R2 0 R3
pmaddwd mm6, mm4
; mm6 = G23 B23
punpckldq mm4, mm7
; mm4 = 4 1 2 3
pmaddwd mm0, mm4
; mm0 = R41 R23
and eax, 0ffffh
; take modulo 256x256 for point 4
paddd mm5, mm6
; mm5 = G B
pand mm5, reg_clr2
; clear out appropriate bits for 16 bit conversion
NOP
; not necessary, but inserted to guarantee 3 cyles
; for mm0 before accessed
punpckldq mm4, mm0
; mm4 = R23 -
paddd mm4, mm0
; mm0 = R -
punpckhdq mm6, mm5
; mm6 = G -
pand mm4, reg_clr3
; clear appropriate bits for 16 bit conversion
psrld mm5, 17
; B is correct position
psrlq mm6, 43
; G is correct position
movq mm0, mm1
; make another copy of u, v for modification
psrlq mm4, 38
; R in correct position
por mm5, mm6
; B and G in correct position
por mm4, mm5
; final result in mm0
paddd mm1, mm2
; performs u = u + du and v = v + dv
movd edx, mm4
; move result to edx
paddd mm2, reg_dduv
; performs du1 = du0 + ddu, dv1 = dv0 + ddv
mov [ecx], dx
; write result to destination image
add ecx, 2
; move to next pixel for next iteration
dec num_of_pixels
; check counter
jnz biquad
emms
; clear floating point stack
ret
bilinear_quadratic ENDP
END
APPENDIX B: MMX
Code for Variable texture size
This version of code allows a variable texture size, from 16x16
to 256x256. It is not optimized for pairing.
TITLE bilquad
; prevent listing of iammx.inc file
.nolist
INCLUDE iammx.inc ; MMX technology assembly Macros
.486P
.model FLAT
;******************************* **********************************
; Data Segment Declarations
;******************************* **********************************
.DATA
reg_clr2 DWORD 003e0000h,
003f0000h
reg_clr3 DWORD 00000000h,
003e0000h
reg_clr4 DWORD 0000fc00h,
0f800f800h
reg_clr5 DWORD 0000ffffh,
0000ffffh
reg_clr6 DWORD 000000ffh,
000000ffh
reg_xoru1 DWORD 7fff7fffh,
7fff7fffh
reg_xorv1 DWORD 00007fffh,
00007fffh
reg_xorv2 DWORD 7fff0000h,
7fff0000h
reg_dduv DWORD 00000000h,
00000000h
reg_mult0 DWORD 0h,
0h
reg_mult1 DWORD 0h,
0h
reg_mult2 DWORD 0h,
0h
reg_mask1 DWORD 0h,
0h
reg_mask2 DWORD 0h,
0h
;***********************************************************************
; Constant Segment Declarations
;***********************************************************************
.const
;***********************************************************************
; Code Segment Declarations
;***********************************************************************
.code
COMMENT ^
void bilinear_quadratic (
int32 *texel_ptr,
int32 *dest_ptr,
int32 *color_pal,
int32 num_of_pixels,
int32 u,v,du,dv,ddu,ddu
int32 text_size);
^
bilinear_quadratic PROC NEAR C USES edi esi ebx,
texel_ptr:PTR
SDWORD, dest_ptr:PTR SDWORD,
color_pal:PTR
SDWORD,
num_of_pixels:DWORD,
u:DWORD,
v:DWORD, du:DWORD, dv:DWORD,
ddu:DWORD,
ddv:DWORD, text_size:DWORD,
text_size_bits:DWORD
; set up bits to allow tiling calculation
mov ecx, text_size_bits
; determines number of bits to shift
mov eax, text_size
; copy texture size(integer) to register
mov reg_mask1, eax
sub reg_mask1, 1
; mask bits for u
shl eax, cl
; shift to get mask bits for (linear address)
sub eax, 1
; final result of mask bits (for u and v)
mov reg_mask2, eax
; move mask bits to memory to free up register
; move commonly used pointers to registers/initialization
movq mm1, u
; copy u to mmx register (16.16 value)
movq mm2, du
; copy du value to mmx register (16.16 value)
punpckldq mm1, v
; copy u and v in mm1 register (64 bits)
punpckldq mm2, dv
; copy du and dv into one mmx register
movq mm0, mm1
; make another copy of u, v for mod.
movq mm7, mm1
; copy u and v for integer part conversion
movq mm3, ddu
; copy ddv value to mmx register
punpckldq mm3, ddv
; copy ddu and ddv to one mmx register
movq reg_dduv, mm3
; reg_dduv = ddv ddu
; calculate uv index in linear texel map array
psrld mm7, 16
; get integer part of v and u
movd eax, mm7
; eax = u
psrlq mm7, 32
; mm7 = 0 v
movd ebx, mm7
; ebx = v
shl ebx, cl
; calculate vertical offset
or eax, ebx
; linear address in eax
; ===========================================================
; calculate the weighted values used to multiply the RGB values
; for each texel point
; Objective: multiply mm0 = u u ~u ~u by mm4 = v ~v v ~v put put
; result in mm0
pand mm0, reg_clr5
; clear out integer part
psrld mm0, 7
; shift u and v by 7 bits to expose fractionalpart
movq mm4, mm0
; make a copy for the other operand
punpcklwd mm0, mm0
; mm0 = - - u u
punpckhwd mm4, mm4
; mm4 = - - v v
punpckldq mm0, mm0
; mm0 = u u u u
punpckldq mm4, mm4
; mm4 = v v v v
movq mm3, mm4
; mm3 = v v v v
pxor mm4, reg_xorv2
; 1's complement mm4 = ~v v ~v v
pmulh mm4, mm0
; mm4 = 2 3 2 3
pxor mm3, reg_xorv1
; 1's complement mm3 = v ~v v ~v
pxor mm0, reg_xoru1
; mm0 = ~u ~u ~u ~u
pmulhw mm3, mm0
; mm3 = 4 1 4 1
movq reg_mult0, mm3
; reg_mult0 = 4 1 4 1
movq reg_mult1, mm4
; reg_mult1 = 2 3 2 3
punpckldq mm4, mm3
; mm4 = 4 1 2 3
movq reg_mult2, mm4
; reg_mult2 = 4 1 2 3
mov esi, texel_ptr
; move texture image pointer to register
mov edi,color_pal
; move color pallette base pointer to register
biquad:
xor edx, edx
; avoid partial stalls
mov dl, [esi][eax]
; get color pallette pointer of point 1
movq mm5, [edi][edx*4]
; get RGB of point 1 from color pallete
add eax, text_size
; increment v to find point 4
and eax, reg_mask2
; mask out carry bits (tiling)
xor edx, edx
;
mov dl, [esi][eax]
; get color pallette index of point 4
punpcklbw mm5,[edi][edx*4]
; get RGB of point 4 from color pallete
; mm5 = 0 0 R4 R1 G4 G1 B4 B1
add eax, 1
; u = u + 1
and eax, reg_mask1
; mask out carry bits(tiling)
or eax, ebx
; calculate point 3 index
add eax, text_size
; increment v
and eax, reg_mask2
; mask out carry bits (tiling)
xor edx, edx
;
mov dl, [esi][eax]
; get color pallete index of point 3
movq mm6, [edi][edx*4]
; get RGB of point 3 from color pallete
sub eax, text_size
; v = v - 1
and eax, reg_mask2
; mask out borrow bits(tiling)
xor edx, edx
;
mov dl, [esi][eax]
; get color pallete index of point 2
punpcklbw mm6, [edi][edx*4]
; get RGB of point 2 from color pallete
; mm6 = 0 0 R2 R3 G2 G3 B2 B3
pxor mm7, mm7
; clears mm7 for use in subsequent instr.
; arrange RGB values in proper format for parallel multiply
movq mm3, mm5
; mm3 = mm5 = 0 0 R4 R1 G4 G1 B4 B1
punpcklbw mm5, mm7
; mm5 = 0 G4 0 G1 0 B4 0 B1
movq mm0, mm6
; mm0 = mm6 = 0 0 R2 R3 G2 G3 B2 B3
punpcklbw mm6, mm7
; mm6 = 0 G2 0 G3 0 B2 0 B3
punpckhwd mm0, mm3
; mm0 = 0 0 0 0 R4 R1 R2 R3
punpcklbw mm0, mm7
; mm0 = 0 R4 0 R1 0 R2 0 R3
pmaddwd mm5, reg_mult0
; mm5 = G41 B41
pmaddwd mm6, reg_mult1
; mm6 = G23 B23
pmaddwd mm0, reg_mult2
; mm0 = R41 R23
punpckldq mm4, mm0
; mm4 = R23 -
paddd mm5, mm6
; mm6 = G B
paddd mm0, mm4
; mm0 = R -
; converts 24 bit color to 16 bit color
pand mm5, reg_clr2
pand mm0, reg_clr3
punpckhdq mm7, mm5
; mm7 = G -
psrld mm5, 17
; B is correct position
psrlq mm7, 43
; G is correct position
por mm5, mm7
; B and G in correct position
psrlq mm0, 38
; R in correct position
por mm5, mm0
; final result in mm3
; quadratic approximation -->
; calculate next texel point for next iteration
paddd mm1, mm2
; performs u = u + du and v = v + dv
paddd mm2, reg_dduv
; performs du1 = du0 + ddu, dv1 = dv0 + ddv
; ===========================================================
; calculate the weighted values used to multiply the RGB values
; for each texel point
; Objective: multiply mm0 = u u ~u ~u by mm4 = v ~v v ~v put put
; result in mm0
movq mm0, mm1
; make another copy of u, v for modification
pand mm0, reg_clr5
; clear out integer part
psrld mm0, 7
; shift u and v by 6 bits to expose fractionalpart
movq mm4, mm0
; make a copy for the other operand
punpcklwd mm0, mm0
; mm0 = - - u u
punpckhwd mm4, mm4
; mm4 = - - v v
punpckldq mm0, mm0
; mm0 = u u u u
punpckldq mm4, mm4
; mm4 = v v v v
movq mm3, mm4
; mm3 = v v v v
pxor mm4, reg_xorv2
; 1's complement mm4 = ~v v ~v v
pmulhw mm4, mm0
; mm4 = 2 3 2 3
pxor mm3, reg_xorv1
; 1's complement mm3 = v ~v v ~v
pxor mm0, reg_xoru1
; mm0 = ~u ~u ~u ~u
pmulhw mm3, mm0
; mm3 = 4 1 4 1
movq reg_mult0, mm3
; reg_mult0 = 4 1 4 1
movq reg_mult1, mm4
; reg_mult1 = 2 3 2 3
punpckldq mm4, mm3
; mm3 = 4 1 2 3
movq reg_mult2, mm4
; reg_mult2 = 4 1 2 3
; commit final result( 16 bit RGB value) to memory
mov ebx, dest_ptr
; move image poiner to register
add dest_ptr, 2
; move to next pixel for next iteration
movd edx, mm5
; move result to edx
mov [ebx], dx
; write result to destination image
; calculate uv index in linear texel map array
movq mm7, mm1
; copy uv
psrld mm7, 16
; get integer part of v and u
movd eax, mm7
; eax = u
and eax, reg_mask1
; allow only 256x256 texture size
psrlq mm7, 32
; mm7 = 0 v
movd ebx, mm7
; ebx = v
shl ebx, cl
; calculate vertical offset
or eax, ebx
; linear address in eax
dec num_of_pixels
; check counter
jnz biquad
emms
; clear floating point stack
ret
bilinear_quadratic ENDP
END
APPENDIX C: C
version of inner loop
//-------- Header file -----------------
#ifndef _struct_texel_pixel
#define _struct_texel_pixel
#include <stdio.h>
typedef struct _texel { _int8 unsigned index; } texel;
typedef struct _pixel { _int16 unsigned color16;} pixel;
typedef struct _colorpal {
_int8
unsigned Bcolor;
_int8
unsigned Gcolor;
_int8
unsigned Rcolor;
_int8
unsigned dummy; // dummy value to enable 32 bit alignment
} color_pal;
#endif
extern void bilinear_quadratic();
//-------- Main Program -----------------
#include <stdlib.h>
#define reg_clr1 0x00f8
#define reg_clr2 0x00fc
#define whole_part 1
#define frac_part 16
#define reg_mod1 0xffff
#define reg_mod2 0x00ff
#define reg_mod3 0xff00
#define stride 256 // 256 X 256 matrix
#define log2stride 8
// this procedure performs binlinear interpolation and quadratic
// approximation
// for texture mapping with perspective corrrection.
void bilinear_quadratic(
texel
*texel_ptr, //texture pointer to a 256x256 bit map
pixel
*destin_ptr, //dest pointer to scanline (16 bits/pixel)
color_pal
*color, //ptr to palette (24 bits/pixel)
int32
num_of_pixels, //number of pixels per scanline
int32
u, v, du, dv, ddu,
int32
ddv) // texture map coordinates, fixed point
{
_int32
u_coord, v_coord; // integer part of u,v coordinate
_int32
u_frac, v_frac; // fractional part of u,v coordinate
_int32
pt1, pt2, pt3, pt4; // weighted values for each of the four
//
points in texel map
_int32
R_color1, R_color2, R_color3, R_color4; // RGB color values
//for
each of 4 points
_int32
G_color1, G_color2, G_color3, G_color4;
_int32
B_color1, B_color2, B_color3, B_color4;
_int32
temp_R, temp_G, temp_B;
_int32
u_acc, v_acc, du_acc, dv_acc;
_int32
tmp, index1, index2, index3, index4;
_int32
loc2, loc3, loc4;
int
count;
_int32
tp1,tp2;
// copy memory values to registers
u_acc = u;
v_acc = v;
du_acc = du;
dv_acc = dv;
count = 0;
// loop through each pixel and use bilinear interpolation to
// map texture and use quadratic approximation to get next texel
while (count < num_of_pixels) {
// get fractional part of u and v
u_frac = u_acc;
v_frac = v_acc;
u_frac = u_frac >> whole_part;
v_frac = v_frac >> whole_part;
// get integer part of u and v
u_coord = u_acc;
v_coord = v_acc;
u_coord = (u_coord >> frac_part) & reg_mask2;
v_coord = (v_coord >> frac_part) & reg_mask2;
// weighted values due to u and v coordinate
tp1 = ~v_frac;
tp2 = ~u_frac;
// make it signed
u_frac = u_frac & 0x7fff;
v_frac = v_frac & 0x7fff;
tp1 = tp1 & 0x7fff;
tp2 = tp2 & 0x7fff;
pt2 = (_int32) (u_frac * tp1);
pt1 = (_int32) (tp2 * tp1);
pt3 = (_int32) (u_frac * v_frac);
pt4 = (_int32) (tp2 * v_frac);
// result is in upper word
pt1 = pt1 >> 16;
pt2 = pt2 >> 16;
pt3 = pt3 >> 16;
pt4 = pt4 >> 16;
// get index to color pallette
tmp = u_coord + (v_coord << log2stride);
loc4 = tmp + stride;
loc4 = loc4 & reg_mod1; // tiling
u_coord = u_coord + 1;
u_coord = u_coord & reg_mod2; // tiling
v_coord = v_coord + 1;
v_coord = v_coord & reg_mod2; // tiling
loc3 = u_coord + (v_coord << log2stride);
loc2 = loc3 + reg_mod3;
loc2 = loc2 & reg_mod1; // tiling
// read in texel value (index to color pallette)
// all these values are 8 bit unsigned integer
index1 = texel_ptr[tmp].index;// palette index for point 1
index2= texel_ptr[loc2].index;// palette index for point 2
index4= texel_ptr[loc4].index;// palette index for point 4
index3= texel_ptr[loc3].index;// palette index for point 3
// make index values positive signed 16 bit integer
index1 = index1 & 0x00ff;
index2 = index2 & 0x00ff;
index3 = index3 & 0x00ff;
index4 = index4 & 0x00ff;
// read in RGB values for each texel (8 bit unsigned integer
R_color1 = (color[index1].Rcolor) & 0x00ff; // texel pt1
R_color2 = (color[index2].Rcolor) & 0x00ff; // texel pt2
R_color4 = (color[index4].Rcolor) & 0x00ff; // texel pt4
R_color3 = (color[index3].Rcolor) & 0x00ff; // texel pt3
G_color1 = (color[index1].Gcolor) & 0x00ff; // texel pt1
G_color2 = (color[index2].Gcolor) & 0x00ff; // texel pt2
G_color4 = (color[index4].Gcolor) & 0x00ff; // texel pt4
G_color3 = (color[index3].Gcolor) & 0x00ff; // texel pt3
B_color1 = (color[index1].Bcolor) & 0x00ff; // texel pt1
B_color2 = (color[index2].Bcolor) & 0x00ff; // texel pt2
B_color4 = (color[index4].Bcolor) & 0x00ff; // texel pt4
B_color3 = (color[index3].Bcolor) & 0x00ff; // texel pt3
//****************************************************************
// calculate new color value for each pixel //****************************************************************
// readjust value because multiplier was shifted right 2 times
R_color1 = R_color1 << 2;
R_color2 = R_color2 << 2;
R_color3 = R_color3 << 2;
R_color4 = R_color4 << 2;
R_color1 = (_int32) (R_color1 * pt1);
R_color2 = (_int32) (R_color2 * pt2);
R_color3 = (_int32) (R_color3 * pt3);
R_color4 = (_int32) (R_color4 * pt4);
temp_R = R_color1 + R_color2 + R_color3 + R_color4;
// readjust value because multiplier was shifted right 2 times
G_color1 = G_color1 << 2;
G_color2 = G_color2 << 2;
G_color3 = G_color3 << 2;
G_color4 = G_color4 << 2;
G_color1 = (_int32) (G_color1 * pt1);
G_color2 = (_int32) (G_color2 * pt2);
G_color3 = (_int32) (G_color3 * pt3);
G_color4 = (_int32) (G_color4 * pt4);
temp_G = G_color1 + G_color2 + G_color3 + G_color4;
// readjust value because multiplier was shifted right 2 times
B_color1 = B_color1 << 2;
B_color2 = B_color2 << 2;
B_color3 = B_color3 << 2;
B_color4 = B_color4 << 2;
B_color1 = (_int32) (B_color1 * pt1);
B_color2 = (_int32) (B_color2 * pt2);
B_color3 = (_int32) (B_color3 * pt3);
B_color4 = (_int32) (B_color4 * pt4);
temp_B = B_color1 + B_color2 + B_color3 + B_color4;
// integer result in upper byte
temp_R = temp_R >> 16;
temp_G = temp_G >> 16;
temp_B = temp_B >> 16;
// convert to 16 bit color assume 0RGB
temp_R = temp_R & reg_clr1;
temp_G = temp_G & reg_clr2;
temp_B = temp_B & reg_clr1;
temp_R = temp_R << 8;
temp_G = temp_G << 3;
temp_B = temp_B >> 3;
temp_R = temp_R | temp_G | temp_B;
destin_ptr[count].color16 = (short) temp_R;
// caculate next texel using du, dv, ddu, and ddv
// Quadratic Approximation
u_acc = u_acc + du_acc;
v_acc = v_acc + dv_acc;
du_acc = du_acc + ddu;
dv_acc = dv_acc + ddv;
// loop count
count++;
} // end while loop
} // end bilinear_quadratic()