|
|
|
|
|
|
|
|

|
Notice Copyright © Intel Corporation (1996). Third-party brands and names are the property of their respective owners.
|
Intel Developer Relations Group
Version 1.0
November 18, 1996
1.0 Introduction
For 3D graphics, texture
mapping adds realism to a scene. Texture mapping
involves "wrapping" a 2D image around a computer-generated
3D object, to give the appearance that the object is composed of
a particular material, or is far more complex than the underlying geometric
description. Currently, two types of texture mapping
exist. One is image texture mapping and the other is procedural
texture mapping.
With today's processors and graphics memory size limits, real-time calculations of textured 3D scenes tend to be slow. Two faster methods are addressed here. The first is to process information in parallel, using the SIMD technique available on MMX(tm) technology processors. The second is to use procedural textures instead of image texture mapping.
Image texture mapping transforms or warps a pre-drawn image onto an object, taking into account the foreshortening and resizing based on the object's orientation in the 3D world. Procedural texture mapping uses a mathematical approach to "create" an image on an object. Rather than use a pre-drawn image, a mathematical algorithm generates the image in real-time. Both approaches have advantages and disadvantages. The procedural mathematics shown here are a modified version of Dr. Ken Perlin's noise basis function. [See " Texturing and Modeling, A Procedural Approach " by David S. Ebert, F. Musgrave, D. Peachey, Ken Perlin, and Steven Worley, published by Academic Press, Boston, 1994]
The function makes textures, such as grass, water, snow, stars, and marble. The noise basis function is an important underlying factor in procedural texture mapping, generating images such as Figures 1.0-1.3. Further, the noise function can serve as the building block for many unique procedural textures. For example, see the marble-like textures in figures 1.4 - 1.5 and figure 2.1.
This paper gives the reasons for using Dr. Ken Perlin's Noise function, along with target applications. MMX code along with the corresponding C code is given for the algorithm. Finally, measured performance and possible improvements are presented.
With a procedural texture, there is no need to load and continually reference a pre-defined image into memory, and thus procedural textures are not limited by memory bandwidth. Our performance goal for this algorithm is 5 to 10 million pixels per second (15 to 30 Frames/sec for a 640x480 pixel window). Secondly, using a mathematical algorithm instead of a pre-drawn image allows zooming in and out, without significant degradation in quality.
The highly-optimized MMX code herein requires approximately 32 clocks per pixel, adequate for real-time 3D texturing on large portions of a full-screen-scene.
1.1 Target

MMX Technology Noise, MTN, is targeted at assembly
language programmers using MMX technology. MTN was developed and tested on
DirectX 3 under Microsoft Windows* 95
(but could be applied elsewhere), and will texture a surface one scanline at a time.
This benefits games, VR simulations, flight simulators, auto racing,
fighting games, or anything involving real-time 3D or 2D graphics. Since
procedural texturing supports an infinite zoom without loss of detail, flight
simulators benefit most from this technology. For example, it is possible
to approach a grassy field close up in an airplane and not lose detail in the scene.
1.2 Output
Examples of the MTN function output are shown below. The grass of
Figures 1.0 and 1.1 consists of 256 shades of greens from a palette.
Multiple palettes can be used to give different looks for several
regions of grass; for example, tan or brown tones to give a sandy
appearance. NOTE that this is a software
palette contained totally within the MTN function, not related to the
Windows* system palette.


| Figure 1.0: Astro-Turf or Grass | Figure 1.1: Zoomed in detail from figure 1.0 |
As seen in Figures 1.0 - 1.1, the use of a mathematical algorithm allows for zoom-in without blockiness, unlike conventional texture mapping. Figures 1.2 and 1.3 show how changing the colors in the palette, zoom levels, and texture orientation give different effects.


| Figure 1.2: Water waves. | Figure 1.3: Nighttime stars or falling snow? |
By adding extra code to Perlin's noise basis function, the marble-like textures in figures 1.4 and 1.5 can be produced. To generate the marble, imagine starting with vertical stripes of light and dark blue colors. To create the wavy effect, the noise function adds a random offset to the original color. For each pixel, a weighted average of the original color and the noise generates the wavy effect. By varying the weights used for the original color and the noise, the waviness can be controlled.


| Figure 1.4: Marble #1 - Using vertical stripes and noise. | Figure 1.5: Marble #2 - Using vertical and horizontal stripes with noise. |
For the marble in figure 1.5, the above technique is used not only in the vertical direction but also in the horizontal direction. Then the two color components are summed together.
2.0 Overview
Grass and water were chosen for texture generation because of the commonality.
Algorithms for drawing realistic grass pose problems due to the complicated
modeling. The algorithm also needs to be parallel to take advantage of MMX
technology. MMX technology uses a Single Instruction Multiple
Data (SIMD) technique to speed up software, by processing multiple
data elements in parallel.
To achieve the grass-like effect, the original algorithm used "fractional Brownian motion", fBm, by F. Kenton Musgrave. This algorithm is based on an iterative method which sums different (Perlin) noise values together. To explain how the fBm works, imagine an image just like figure 1.1, treated as a heightmap. In other words, the colors in the image represent actual heights. Therefore, by looking at the image from the side, an imaginative person might see rolling hills and mountains. Now, repeat this image many times. For each copy of the image, scale the amplitude of the heights of the hills by varying amounts. Next, vary the zoom factor of the scene for each image. Some scenes might be zoomed out, while other scenes might be zoomed in. Lastly, to form the final image, sum the images together. See figure 2.1 for an output example.
The number of iterations of Perlin's noise in the fBm are known as "Octaves". Musgrave suggests the number of octaves used should be:
octaves = log_base2(screen.resolution) - 2
For a screen resolution of 640x480,
octaves = log_base2(640) - 2 = ~7 octaves
This is a general rule to follow. Usually, fewer octaves produces an image close to the original and requires less computation time.
The final image produced by fBm when using 7 octaves is shown in Figure 2.1:

The following diagram shows how the image in figure 2.1 was built. Seven noise function outputs are scaled and summed together. Under each of the noise images lists the range of the texture space along with the amplitude modification factor. In practice, experiments showed octaves beyond 3 were essentially unneeded.
 +
+  +
+
 +
+  +
+
 +
+  +
+
 =
= 
| Noise #0 | Noise #1 | Noise #2 | Noise #3 | Noise #4 | Noise #5 | Noise #6 | fBm, 7 oct |
| S = 1 | S = 2 | S = 4 | S = 8 | S = 16 | S = 32 | S = 64 | |
| A = 1.000 | A = 0.500 | A = 0.250 | A = 0.125 | A = 0.0625 | A = 0.03125 | A = 0.015625 |
The use of several octaves is a problem in terms of real-time calculation. To simplify the calculations, only the noise basis function will be programmed using MMX technology. Perlin's noise basis function provides adequate detail for randomness, while Musgrave's fBm routine is overkill. In fact, Perlin's noise basis function can be derived from the fBm function by using only one octave. Thus the algorithm shown here will generate only the first image (Noise #0) in figure 2.2.
2.1 Algorithm Criteria
A good noise function needs to produce either a 2d texture or 3d volume with a
varying pattern. For simplification purposes, only the 2d texture noise function
will be explained. This noise pattern needs to be chaotic and random in nature
yet still be under some control.
The function used to generate the noise pattern needs to be continuous. This
adds a smooth quality to the overall texture. Figures 1.0 and 1.1 show typical
output from 2D noise functions.
Any good texture must remain oriented correctly on the objects (polygons) it is drawn on in 3D -- it should rotate with them, so that the grass or sea does not change orientation as a flight simulator engages in a roll. It should also shrink or blur in perspective like railroad tracks converging in the distance.
As seen in figure 2.2, Perlin's Noise Basis Function is used as a building block to build the more complicated Fractional Brownian Motion. The Noise Basis Function plays an important part in procedural texturing and is routinely used to generate other textures besides fBm. See figures 1.4 and 1.5.
Therefore this application note focuses on the Noise Basis function developed by Dr. Ken Perlin and not on Fractional Brownian Motion.
3.1 Algorithm Description
According to Dr. Ken Perlin, "Ideally the noise function would be constructed
by blurring white noise, preferably by convolving with some Gaussian kernel"
[See "
Texturing and Modeling,
A Procedural Approach " by David S. Ebert, F. Musgrave, D. Peachey,
Ken Perlin, and Steven Worley, published by Academic Press, Boston, 1994, page 196].
Since this is impracticable in terms of computer computation, a faster alternative
needed to be devised. This is where Dr. Ken Perlin came up with the idea of a
noise basis function. This function is an approximation to the original and
complicated Gaussian kernel idea. The next section explains the overall basis
of his algorithm.
Dr. Ken Perlin's noise basis algorithm works in both 2D and 3D. Since MTN is designed only for the 2D case, this will be explained. First, lets say we have a point in a flat plane that is our texture-mapping space. The goal of this is to determine the color of the point. We take a bounding square and surround the point with it. Therefore, the (u,v) point of the texel is inside the square. Now, the square is placed so that the corner points all lie on integer boundaries. (The x, y component of each of the corner points of the square are whole numbers). The distance from one side to the other side of the square will be one unit, as in Figure 3.1. Remember, the yellow area is the infinite texture mapping space.
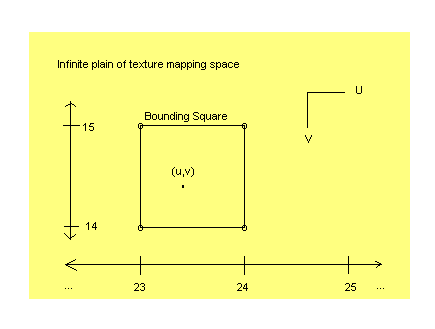 |
| Figure 3.1 - Bounding Square |
Imagine that there are vectors that extend from the square corner points to the texel. See figure 3.2.
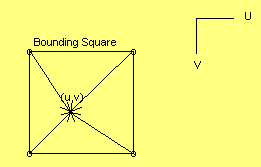 |
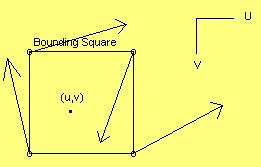 |
| Figure 3.2 - Point vectors | Figure 3.3 - Unit length gradient vectors |
A second set of vectors also extends from the corner points of the square. These vectors, called gradient vectors, all have a length of one unit and are uniformly distributed (The chances of them pointing in a certain direction verses another direction are the same). See figure 3.3.
The algorithm takes the dot product of each randomly-chosen gradient vector with its corresponding point vector. The dot product of two vectors can be represented by the following equation:
dot(Vector_A, Vector_B) = (Au)i * (Bu)i + (Av)j * (Bv)j.
The result will be a scalar and not a vector. After performing four dot products (one for each corner), the resulting scalar values will be the colors for each corner point of the square.
Last, the color of the texel inside the square can be found by interpolating the four corner points in the U and V direction.
3.2 The Color Array (256 color palette)
The MTN (MMX Technology Noise) function calculates an index value
for the color, rather than determining the color directly. The
index value is then used to obtain the color to put on the screen
from an array. This approach assumes that the colors in the array
form a continuing spectrum.
The colors in the array can be set up as 8 bit palletized, 555, 565, or 888 format depending on the hardware and drivers present on the machine. For example, if the computer used RGB555 color format, each of the 256 entries in the array will be in 555 (16-bit) format. Or for 8-bit palletized, the index value can be used directly as the frame buffer pixel (which the hardware palette will then translate onto the screen).
The sample program works in Windows 16 bit screen mode (555 and 565 color formats). The program will not work in 8 bit palletized mode and 24 bit true color. To support these screen modes, parts of the code need to be changed, as described in Microsoft's DirectDraw documentation.
By choosing appropriate colors for the palette and correct zoom, the algorithm can be used for other textures besides grass. For example, a palette with mostly black colors and a few whites can be used to simulate stars in the night-time sky. Or a palette with blue hues can be used to simulate water in a pond. A disadvantage to this approach is that the texture mapping routine must use an array, which limits parallelism. Parallelism can be achieved by replacing the array with a mathematical color-calculation algorithm, but flexibility is then lost. Appropriate sections in the code are marked so the programmer knows where to add such code.
3.3 Function Parameters
The MMX Technology Noise function accepts 32-bit fixed-point texel
coordinates (u, v) and writes pixels to the display or memory buffer,
for a scanline Num_Pix long. The algorithm uses fixed point integer mathematics.
The output is 16-bit RGB, but could be 8-bit palletized or 24-bit RGB with
minimal changes. The size of the u, v, du, dv, ddu, and ddv inputs
determines the "zoom factor". The ddu and ddv parameters measure the rate of
change of du and dv per pixel drawn. For true perspective corrected textures, two
divisions per pixel are required. Since this would be slow for real-time
performance, the ddu and ddv inputs are used to approximate it via simple
addition.
There are 9 parameters passed to MTN. They are listed below
with a brief explanation. All parameters are DWORDs (32 bits).
Six of the input parameters to the function are in 10.22 format.
Conversion from 10.22 format to 16.16 format is possible by shifting
the bits to the right 6 places or dividing by 2^6 = 64.
From the authors experience, 16.16 format is not recommended because it does not have enough accuracy to produce a good image. The texel coordinate information (u, v) and the delta values (du, dv, ddu, ddv) are maintained in the 10.22 format. This is to assure that the error in accuracy which grows with subsequent additions of du to u and dv to v is kept small. 10.22 format also allows for enough precision to accurately represent ddu and ddv terms. The algorithm though, only uses 16 bits of the original 32 bits for u and v.
| u_init, v_init: | Starting u and v parameters of texture space. | (10.22 format) |
| du, dv: | Change in u_init and v_init per pixel across the scanline. | (10.22 format) |
| ddu, ddv: | Change in du and dv per pixel, for perspective correction. | (10.22 format) |
| Num_Pix: | Number of pixels in the scan line to draw. | (unsigned long) |
| palette: | Pointer to the 256 color palette. | (pointer to _int16) |
| screen_buffer: | Pointer to the start of the scan line in the screen buffer. | (pointer to _int16) |
As said before, ddu and ddv are perspective correction terms used to approximate the change in the du and dv terms. For more information on the use of ddu and ddv, please see the Intel application note on MMX(tm) Technology and Bilinear Filtering.
Basing the calculation on u and v, instead of x and y, was done to allow rotation of the texture. Mapping to a consistent texture coordinate system allows the texture to stay aligned with the polygon edges even if the polygon is rotated.
4.0 Performance
The original version of the algorithm written with
MMX technology calculates the values for two pixels at once.
For performance gains, the algorithm is used to calculate
the colors for the odd numbered pixels. The even numbered
pixels are derived from neighboring odd pixels. This allows the
algorithm to calculate four pixel values through one pass of the
inner loop. The inner loop of the final algorithm requires 128 clock
cycles to determine four pixel values (or 32 clocks per pixel).
For performance comparisons, statistical information is also listed
for the "C" implementation of the algorithm and a comparison is made using
one other texture mapping technique. The other technique used for
comparison is Intel's
MMX(tm)
Technology and Bilinear Filtering
routine written in MMX Technology assembly.
Intel's MMX Technology and Bilinear Filtering routine was chosen for comparison (instead of point sampling for example) because it produces final images similar in quality to the MMX Technology Noise. For most resolutions of MMX Technology Noise, filtering is not needed because the image is calculated "smoothly", achieving quality close to Bilinear Filtering.
| MMX code (4 pixels per loop): | 32 clocks per pixel |
| Perlin's C code (2 pixels per loop): | 343 clocks per pixel. |
| Intel's Bilinear Filtering - Assembly (1 pixel per loop): | 48 clocks per pixel. |
| MMX code (4 pixel loop version): | 58 clocks per function call if 4 or more pixels will be drawn. Add 7 more clocks if the scanline isn't a multiple of four pixels. |
| Perlin's C code (2 pixel loop version): | 32 clocks per function call. |
| Intel's Bilinear Filtering: | 30 clocks per function call. |
| MMX code (4 pixel loop version): | 27 memory accesses to draw 4 pixels. Approx 7 accesses/pixel. 4 of the 27 involve arrays of 512 bytes each. |
| Perlin's C code (2 pixel loop version): | 132 |
| Intel's Bilinear Filtering(1 pixel loop version): | 19 memory accesses to draw 1 pixel. 4 of the 19 involve arrays of 512 bytes each. 4 of the 19 involve accesses to a texture map. |
4.4 Performance Results, from VTune:
| Func Name | Instructions | % Pairing |
| MMX (4 p) | 290 | 75 |
| Perlin's C code | 204 | 44 |
| Intel's Bilinear filtering code | 116 | 78 |
The next few tables list various scanline lengths for the different algorithms and the number of clock cycles required of each. Note, the values reported are from a VTune static analysis, not dynamic.
Measured clocks for MMX Technology Noise:
| Scan len: | 1 | 2 | 3 | 4 | 10 | 20 | 40 | 60 | 80 | 100 | 140 | 180 | 220 |
| Clocks: | 34 | 39 | 44 | 187 | 331 | 699 | 1339 | 1979 | 2619 | 3259 | 4539 | 5819 | 7099 |
| Ave Clock/Pixel: | 34.0 | 19.5 | 14.7 | 46.8 | 33.1 | 35.0 | 33.5 | 33.0 | 32.7 | 32.6 | 32.4 | 32.3 | 32.3 |
As shown in the above table, as the number of pixels in a scanline increases, the average clocks per pixel approaches 32.
Equation used to obtain results:
1) Start off with "Clocks" = 23 (For overhead).
2) If the scanline length is greater than four pixels then add "36" to "Clocks"
3) Next add "128 * (NumberPixels int.divide 4)" to "Clocks"
4) If "NumberPixels mod 4" is greater than 0, add 6 to "Clocks"
5) Add "5 * (NumberPixels mod 4)" to "Clocks"
The final result in the variable "Clocks" is the total number of clock cycles
required to draw the scanline.
This equation was derived by studying the flow of events in the program based on the number of pixels per scanline.
The pixel averages for the first 3 values in the table are quite low because the leftover pixels at the end of a scanline that aren't multiples of 4 aren't calculated. Instead the last 1, 2, or 3 pixels at the end of the scanline are replicated from the previous pixels drawn.
If there are 3 or less pixels in the scanline, they are mirrored from the pixels drawn in the previous scanline.
Table for Perlin's Optimized "C" code:
Total Clocks Required = 32 + 343 * NumberPixels
| Scan len: | 1 | 2 | 3 | 4 | 10 | 20 | 40 | 60 | 80 | 100 | 140 | 180 | 220 |
| Clocks: | 375 | 718 | 1061 | 1404 | 3462 | 6892 | 13752 | 20612 | 27472 | 34332 | 48052 | 61772 | 75492 |
| Ave Clock/Pixel: | 375.0 | 359.0 | 353.6 | 351.0 | 346.2 | 344.6 | 343.8 | 343.5 | 343.4 | 343.3 | 343.2 | 343.2 | 343.1 |
Table for Intel's Bilinear Filtering:
Total Clock Cycles = 30 + 48 * NumberPixels
| Scan len: | 1 | 2 | 3 | 4 | 10 | 20 | 40 | 60 | 80 | 100 | 140 | 180 | 220 |
| Clocks: | 78 | 126 | 174 | 222 | 510 | 990 | 1950 | 2910 | 3870 | 4830 | 6750 | 8670 | 10590 |
| Ave Clock/Pixel: | 78.0 | 63.0 | 58.0 | 55.5 | 51.0 | 49.5 | 48.8 | 48.5 | 48.4 | 48.2 | 48.2 | 48.2 | 48.1 |
Conclusion: In term's of computation speed, Perlin's Noise Basis Function using MMX Technology is faster than Intel's Bilinear Filtering texture routine. In term's of versatility, Intel's Bilinear Filtering texture routine proves to be the best because it uses pre-drawn images. Therefore, the programmer should use MMX Technology noise where appropriate and let Bilinear Filtering handle the rest.
5.0 Perlin's Original
Noise Basis Function
This section shows a modified form of Dr. Ken Perlin's Noise Basis function.
The code is displayed here for viewing and the next section of the application
note will explain the techniques used to increase performance.
Note: The following code was enhanced for better reading ability. The fundamentals of the code are unchanged however.
#define B 256
static int p[B + B + 2];
static float g2[B + B + 2][2];
static int start = 1;
//***************************************************************************
// Perlin's noise basis function.
// This function is used to generate the smooth texture as seen in
// figures 1.0 and 1.1
//***************************************************************************
void Perlins(long u, long v, long du, long dv, long ddu, long ddv,
unsigned _int16 Num_Pix, unsigned _int16* palette,
unsigned _int16* screen_buffer)
{
unsigned long i;
long bx0, bx1, by0, by1, b00, b10, b01, b11;
long rx0, rx1, ry0, ry1, sx, sy;
long color_p0;
long color_p1;
long color_p2;
long color_p3;
long color_y0;
long color_y1;
long du_inc, dv_inc;
long middle_color, next_color;
static long prev_color = 255;
unsigned long* screen_long_buffer;
screen_long_buffer = (unsigned long*)screen_buffer;
//Special du, dv, ddu, and ddv modification because we're processing
//two pixels at one time.
du = du << 1;
dv = dv << 1;
du_inc = (ddu << 2);
dv_inc = (ddv << 2);
//Initialization - Setup G[][] and P[] arrays (for Gradiant and Permutation);
if (start)
{
start = 0;
initialize();
}
Num_Pix = Num_Pix >> 1;
//Inner loop for the scan line. "Num_Pix" pixels will be drawn.
for (i = 0; i < Num_Pix; i++)
{
//Imagine having a square of the type
// p0---p1 Where p0 = (bx0, by0) +----> U
// |(u,v)| p1 = (bx1, by0) |
// | | p2 = (bx0, by1) | Coordinate System
// p2---p3 p3 = (bx1, by1) V
//The u, v point in 2D texture space is bounded by this rectangle.
//Goal, determine the color of the points p0, p1, p2, p3.
//Then the color of the point (u, v) will be found by linear interpolation.
//First step: Get the 2D coordinates of the points p0, p1, p2, p3.
//Process the x component
bx0 = (u >> 22) & (B - 1);// Integer part of u. x component of p0 and p2
bx1 = (bx0 + 1) & (B - 1);// Integer part of u + 1. x component of p1 and p3
//Process the y component
by0 = (v >> 22) & (B - 1);// Integer part of v. y component of p0 and p1
by1 = (by0 + 1) & (B - 1);// Integer part of v + 1. y component of p2 and p3
//Next, we need vectors pointing from each point in the square above and
//ending at the (u,v) coordinate located inside the square.
//The vector (rx0, ry0) goes from P0 to the (u,v) coordinate.
//The vector (rx1, ry0) goes from P1 to the (u,v) coordinate.
//The vector (rx0, ry1) goes from P2 to the (u,v) coordinate.
//The vector (rx1, ry1) goes from P3 to the (u,v) coordinate.
rx0 = (u >> 14) & 255; // 0.0 <= rx0 < 1.0 or 0 <= rx0 < 255 for fixed math
rx1 = rx0 - 256; // -1.0 < rx1 <= 0.0 or -255 < rx1 <= 0 for fixed math
ry0 = (v >> 14) & 255; // 0.0 <= ry0 < 1.0 or 0 <= ry0 < 255 for fixed math
ry1 = ry0 - 256; // -1.0 < rx1 <= 0.0 or -255 < rx1 <= 0 for fixed math
//Now, for each point p0, p1, p2, p3 in the square above, image having
//a unit gradiant vector pointing in any random direction. This step
//attaches a unit gradiant vector to each point of the square. This is
//done by precalculating 256, random, uniform, unit vectors. Then to attach
//the gradiant vector to a point, an index into the array is needed. The
//index is acquired from the x and y coordinates of the square corner point.
//The algorithm used is called "Folding Over".
//b00, b10, b01, and b11 contain indexes for a gradiant vector for each
//corner of the square shown above.
b00 = p[bx0] + by0;
b10 = p[bx1] + by0;
b01 = p[bx0] + by1;
b11 = p[bx1] + by1;
//Now, for each point in the square shown above, calculate the dot
//product of the gradiant vector and the vector going from each square
//corner point to the (u,v) point inside the square.
color_p0 = rx0 * g[b00][0] + ry0 * g[b00][1];
color_p1 = rx1 * g[b10][0] + ry0 * g[b10][1];
color_p2 = rx0 * g[b01][0] + ry1 * g[b01][1];
color_p3 = rx1 * g[b11][0] + ry1 * g[b11][1];
//Next, calculate the dropoff component about the point p0.
sx = (rx0 * rx0 * (768 - (rx0 << 1))) >> 16;
sy = (ry0 * ry0 * (768 - (ry0 << 1))) >> 16;
//color_p0, color_p1, ... are the colors of the points p0, p1, p2, p3.
//Now use linear interpolation to get the color of the point (sx, sy) inside
//the square.
//Interpolation along the X axis.
color_y0 = color_p0 + ((sx * (color_p1 - color_p0)) >> 8);
color_y1 = color_p2 + ((sx * (color_p3 - color_p2)) >> 8);
//Interpolation along the Y axis.
//Output is from -256 to +256, so a 256 color offset is added and
//the final result is divided by 2. (>>1). 0 <= next_color < 256
next_color = (256 + color_y0 + ((sy * (color_y1 - color_y0)) >> 8)) >> 1;
//Two colors are written to the screen at once. One is calculated
//and the other is averaged from the first. This is done to keep the
//code similar to the MMX(tm) Technology assembly version.
middle_color = (prev_color + next_color) >> 1;
//Write two pixels to the screen buffer.
*(screen_long_buffer) = (palette[next_color] << 16) + palette[middle_color];
screen_long_buffer++; // Advance 1 dword
prev_color = next_color;
u += du + ddu; // New u for calc the color of the next pixel
v += dv + ddv; // New v for calc the color of the next pixel
du += du_inc; // New du for calc the color of the next pixel
dv += dv_inc; // New dv for calc the color of the next pixel
} // End of the scanline - repeat for next pixel
}
//************************************************************************
//Procedure initialize(void)
//The initialize procedure is used to set the parameters in
//arrays g2[][] and p[] used in Perlin's noise basis function.
//************************************************************************
static void initialize(void)
{
int i, j, k;
//The loop sets the numbers in array p[B] equal to the indexes.
//The loop also puts random numbers in array g2[B][2] that range from
// -1/sqr(2) to +1/sqr(2). (-0.707... to +0.707...)
for (i = 0; i < B; i++)
{
p[i] = i;
g2[i][0] = (float)((random() % (B + B)) - B) / B;
g2[i][1] = (float)((random() % (B + B)) - B) / B;
s = sqrt(g2[i][0] * g2[i][0] + g2[i][1] * g2[i][1]);
g2[i][0] = g2[i][0] / s;
g2[i][1] = g2[i][1] / s;
}
//Scramble up the ordered numbers in array p[].
//Array p[] now contains B numbers ranging from 0 to B-1 uniquely.
While (--i)
{
k = p[i];
p[i] = p[j = random() % B];
p[j] = k;
}
//Extra code used to increase the range of the indexes of the array.
//Array p[] and G[][2] now have a valid index ranging from 0 to 2*B.
for (i = 0; i < B + 2; i++)
{
p[B + i] = p[i];
for (j = 0; j < 2; j++)
{
g2[B + i][j] = g2[i][j];
}
}
}
6.1 Programming simplifications used for the Initialize() function:
P[i] = (i * i) mod 256
The above statement requires a "mod" which should not be used. Since the operand of the mod happens to be a power of two (2^8) then the "mod 256" can be replaced with & 255. Therefore, the previous piece of code becomes:
P[i] = (i * i) & 255
The final assembly version of the code will be of the form "P[i] = (i * i) & 65535". This is done because the MMX technology "PMULLW" (16 x 16 bit multiply) instruction will be used.
Therefore to summarize, rather than using arrays P[i] and G2[i], the following algorithms will be used to replace the "initialize()" function:
P[i] = (i * i) & 65535 G2[i] = ((i * i) & 65535) >> 2
This allows us to calculated several results in parallel by using MMX Technology. Array implementation with MMX Technology is possible but hinders the design of the algorithm. The information stored in the MMX registers must be converted from parallel to serial. This is because the information will be indexes into arrays. These indexes must be stored in general purpose registers or offset registers and not MMX registers. Once the information is retrieved from memory, it must be converted back from serial to MMX parallel form. It is the conversion from parallel -> serial -> parallel which makes it difficult to do. Therefore, real-time calculation instead of arrays are used.
6.2 Programming simplifications used for the Noise2()
function:
For this section of the code, not many simplifications
were used. All of the data types were converted over from floating
point to fixed integer 8.8 format -- 8 bits for the
integer part of the number is enough because we only want numbers
in the range 0 to 255. This is evident from the original code
sample:
bx0 = ((int)t) & (B - 1);
7.1 Using all of the above simplifications, here is the final "C" source code:
Note, this program is not optimized for computation speed. For
users wanting to use the "C" implementation of the algorithm, the
author suggests using Perlin's original program. This "C" source is
slower than Perlin's, due to algorithm adaptations which made it possible
to adapt to 16-bit integer for MMX Technology. This code is meant to
be used as a guide, to show how the transition from "C" to assembly
was made.
#define random1(i) ((i * i) & 65535) //GREAT! 1 MMX(tm) instr
#define random2(i) (((i * i) & 65535) >> 2)
//***********************************************************************
//Procedure C_Noise()
//Inputs: u_init, v_init: starting u and v parameters into the image.
// du, dv: the incremental change to u_init and v_init.
// ddu, ddv: the incremental change to du and dv.
// Num_Pix: number of pixels in the scan line to draw.
// screen_buffer: Pointer to the screen buffer.
//Output: 16 bit pixels are drawn to the screen.
//***********************************************************************
void C_Noise(long u_init, long v_init, long du, long dv, long ddu, long ddv,
unsigned _int16 Num_Pix, unsigned _int16* palette,
unsigned _int16* screen_buffer)
{
unsigned char color;
unsigned char bx0, bx1, by0, by1;
unsigned char rx0, ry0;
//FOR ALGORITHM BASED COMMENTS - PLEASE SEE ORIGINAL PROGRAM IN
//SECTION 5.
//Original Perlin's noise program used an array g[512][2].
//This program replaces the array with real-time calculations.
//The results are stored into variables of the form g_b##_#.
_int16 g_b00_0; //Used to replace array g[b00][0]
_int16 g_b00_1; //Used to replace array g[b00][1]
_int16 g_b01_0; //replaces array g[b01][0]
_int16 g_b01_1; //replaces array g[b01][1]
_int16 g_b10_0; //replaces array g[b10][0]
_int16 g_b10_1; //replaces array g[b10][1]
_int16 g_b11_0; //replaces array g[b11][0]
_int16 g_b11_1; //replaces array g[b11][1]
//Used to replace array: b00 = p[p[bx0] + by0];
_int16 b00;
_int16 b01;
_int16 b10;
_int16 b11;
unsigned _int16 i;
unsigned _int16 u_16bit, v_16bit;
signed _int16 rx1, ry1;
signed _int16 sx, sy;
signed long u1, v1, u2, v2;
signed long a, b;
//Inner loop for the scan line. "Num_Pix" pixels will be drawn.
for (i = 0; i < Num_Pix; i++)
{
//Convert the u and v parameters from 10.22 to 8.8 format.
u_16bit = u_init >> 14;
v_16bit = v_init >> 14;
//Same as Perlin's original code except floating point
//is converted over to fixed integer.
bx0 = u_16bit >> 8; //Obtain the integer part of the u coordinate
bx1 = bx0 + 1;
rx0 = u_16bit & 255; //Obtain the fractional part of the u coordinate
rx1 = rx0 - 256;
by0 = v_16bit >> 8;
by1 = by0 + 1;
ry0 = v_16bit & 255;
ry1 = ry0 - 256;
//Same as Perlin's original code except floating point
//is converted over to fixed integer. The ">> 1" is used to
//avoid overflow when the values are multiplied together.
//This is not a problem in "C" but will be in the MMX implementation.
sx = (((rx0 * rx0) >> 1) * ((1536 - (rx0 << 2)))) >> 16;
sy = (((ry0 * ry0) >> 1) * ((1536 - (ry0 << 2)))) >> 16;
//This is where the code differs from Perlins.
//Rather than use arrays p[] and g[][], the values are
//calculated real-time. Here random1() replaces array p[].
//Perlin's equivalent: b00 = p[p[bx0] + by0];
b00 = random1((random1(bx0) + by0));
b01 = random1((random1(bx0) + by1));
b10 = random1((random1(bx1) + by0));
b11 = random1((random1(bx1) + by1));
//Here, random2() replaces array g[][].
//Perlin's equivalent: g_b00_0 = g[b00][0];
g_b00_0 = (random2(b00) & 511) - 256;
g_b01_0 = (random2(b01) & 511) - 256;
g_b10_0 = (random2(b10) & 511) - 256;
g_b11_0 = (random2(b11) & 511) - 256;
g_b00_1 = (random2((b00 + 1)) & 511) - 256;
g_b01_1 = (random2((b01 + 1)) & 511) - 256;
g_b10_1 = (random2((b10 + 1)) & 511) - 256;
g_b11_1 = (random2((b11 + 1)) & 511) - 256;
//Same as Perlin's original code
u1 = rx0 * g_b00_0 + ry0 * g_b00_1;
v1 = rx1 * g_b10_0 + ry0 * g_b10_1;
a = u1 + sx * ((v1 - u1) >> 8);
//Same as Perlin's original code
u2 = rx0 * g_b01_0 + ry1 * g_b01_1;
v2 = rx1 * g_b11_0 + ry1 * g_b11_1;
b = u2 + sx * ((v2 - u2) >> 8);
//Same as Perlin's original code except the output is
//converted from fixed point to regular integer. Also
//since the output ranges from -256 to +256, a 256 offest
//is added to make the range from 0 to 511. This offset
//is the 65536 value. Then the 0 to 511 is scaled down.
//to a range of 0 to 255.
color = (a + 65536 + sy * ((b - a) >> 8)) >> 9;
*(screen_buffer) = palette[color];
u_init += du; // New u for calc the color of the next pixel
v_init += dv; // New v for calc the color of the next pixel
du += ddu; // New du for calc the color of the next pixel
dv += ddv; // New dv for calc the color of the next pixel
screen_buffer++; // Advance 1 word
} // End of the scanline - repeat for next pixel
} // C_Noise()
7.2 The Assembly Source Code (Note, the code is optimized for speed):
Now using the above "C_Noise()" source code as a model, here's the "four pixel version" of the code. The code is optimized for 75% pairing of instructions. Parts of the code might be hard to understand due to the fact that the instructions are rescheduled for pairing optimizations. Comments have been carefully placed to help explain what the contents should be in certain registers at key points in the program. Intel's VTune 2.02 was used to profile the code.
TITLE Modified form of Perlin's Noise Basis function using MMX(tm) technology
;***************************************************************************
;* Copyright Intel Corporation 1996, All Rights Reserved;
;prevent listing of iammx.inc file
.nolist
INCLUDE iammx.inc
.list
.586
.model FLAT
;***********************************************************************
; Data Segment Declarations
;***********************************************************************
DSEG SEGMENT PARA
;KEY for comments
;P0, P1, P# = Pixel number 0, Pixel number 1, Pixel number # respectively.
;Pix = Pixel
;DU = Derivative of the variable U.
;DDU = Derivative of the variable DU.
;Texel = A point in the texture to be mapped onto the screen. Given by U, V.
;Note: Even though the assembly writes four pixel values through each pass of the
;inner loop, only two of the pixels are directly calculated. The other two pixels
;are averaged from neighboring pixels. According to the current scheme,
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MMX = | Pixel #0 | Pixel #1 | Pixel #2 | Pixel #3 |
; +-----------------------------------------------------------+
;Pixels #1 and #3 are directly calculated. Pixel #2 is averaged from Pixel #1 and
;pixel #3. Pixel #0 is averaged from Pixel #1 and the previous pixel before #0.
;
;Also, the programmer realizes that the pixels are labeled from 0, 1, 2, 3 instead
;of 3, 2, 1, 0 as follows the conventional format of Intel Architecture. This was
;an oversite and not realized until it was to late.
;Variables, u, v, du, dv, ddu, ddv each contain parameters for two
;texels. Since u, v, ..., ddv are 64 bit, then each texel parameter is
;32 bit. (32 bit per texel * two texels = 64 bits). This enables us
;to work with two pixels at one time using MMX technology.
ALIGN 8
u QWORD ?
du QWORD ?
ddu QWORD ?
v QWORD ?
dv QWORD ?
ddv QWORD ?
;Since the program only calculates odd pixel values, the even pixel values
;must be averaged. Therefore, for each pass through the inner loop, four
;pixels will be drawn. In order to draw the first pixel, the pixel before
;it must be known for the averaging. This pixel color is contained here.
prev_color DWORD 255
;Various masks. Set up to filter out unwanted bits in MMX registers.
ALIGN 8
mask_32_to_15 QWORD 00007FFF00007FFFh
mask_quad_1 QWORD 0001000100010001h
mask_quad_255 QWORD 00FF00FF00FF00FFh
mask_quad_256 QWORD 0100010001000100h
mask_quad_510 QWORD 01FE01FE01FE01FEh
mask_quad_511 QWORD 01FF01FF01FF01FFh
mask_quad_1536 QWORD 0600060006000600h
mask_double_255 QWORD 000000FF000000FFh
mask_double_FFFF QWORD 0000FFFF0000FFFFh
mask_double_65536 QWORD 0001000000010000h
DSEG ENDS
;***********************************************************************
; Constant Segment Declarations
;***********************************************************************
.const
;***********************************************************************
; Code Segment Declarations
;***********************************************************************
.code
COMMENT^
void MMX_Noise(long u_init, long v_init, long du_init, long dv_init,
long ddu_init, long ddv_init, unsigned long Num_Pix,
unsigned _int16* palette, unsigned _int16* screen_buffer)
^
MMX_Noise PROC NEAR C USES eax ebx ecx edx esi edi,
u_init:DWORD, v_init:DWORD, du_init:DWORD, dv_init:DWORD,
ddu_init:DWORD, ddv_init:DWORD, num_pixels:DWORD,
palette:DWORD, screen_buffer:DWORD
;Initialization
MOV ESI, palette ;ESI will always be pointer to palette
MOV EBX, prev_color
MOV ECX, num_pixels
MOV EDI, screen_buffer ;EDI will always be pointer to screen buffer
MOV EDX, ECX
MOVD MM1, [ESI][EBX*2]
AND ECX, 0FFFFFFFCh
PUNPCKLDQ MM1, MM1 ;If scanline < 4 pix, don't calculate color
SUB EDX, ECX ;EDX= # of leftover pixels at end of scanline
SUB EDI, 8
CMP ECX, 0
JZ start_end_pixels ;Test for scanline lengths less than 4 pix
;Get the UV parameters in MMX(tm) technology form.
;Note: UV texel values are stored in 10.22 fixed integer format.
;This sets up the U parameters for pixels 1 and 3 in MM0 register and
;V parameter in MM1 register. After setup, the registers will contain:
; |--------- 32 bit ------------|
; +-------------------------------------------------------------------+
;MM0 = | U texel for pix #1 = u + du | U texel for pix #3 = u + 3du + 3ddu |
; +-------------------------------------------------------------------+
; +-------------------------------------------------------------------+
;MM1 = | V texel for pix #1 = v + dv | V texel for pix #3 = v + 3dv + 3ddv |
; +-------------------------------------------------------------------+
;This is because the first four pixels drawn on the screen will have the
;U and V texel values of:
;Pixel #0 = u
;Pixel #1 = u + du
;Pixel #2 = u + 2du + ddu
;Pixel #3 = u + 3du + 3ddu
;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged.
MOVD MM0, u_init
SHR ECX, 2 ;ECX= # of times to draw 4 pixels at once
MOVD MM1, v_init
PUNPCKLDQ MM0, MM0 ;U p1 = u, p3 = u
MOVD MM2, du_init
PUNPCKLDQ MM1, MM1 ;V p1 = v, p3 = v
MOVD MM3, dv_init
PADDD MM0, MM2 ;U p1 = u, p3 = u + du
PADDD MM1, MM3 ;V p1 = v, p3 = v + dv
PADDD MM0, MM2 ;U p1 = u, p3 = u + 2du
PADDD MM1, MM3 ;V p1 = v, p3 = v + 2dv
PUNPCKLDQ MM2, MM2
PUNPCKLDQ MM3, MM3
PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du
MOVD MM2, ddu_init
PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv
MOVD MM3, ddv_init
PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du + ddu
PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv + ddv
PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du + 2ddu
PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv + 2ddv
PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du + 3ddu
MOVQ DWORD PTR u, MM0
PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv + 3ddv
MOVQ DWORD PTR v, MM1
;Get the du dv parameters in MMX(tm) technology form
;Note: du dv texel values are stored in 10.22 fixed integer format.
;This sets up the du parameters for pixels 1 and 3 in MM0 register and
;dv parameter in MM1 register. After setup, the registers will contain:
; |--------- 32 bit --------------|
; +---------------------------------------------------------------+
;MM0 = | DU texel for p1 = 4du + 10ddu | DU texel for p3 = 4du + 18ddu |
; +---------------------------------------------------------------+
; +---------------------------------------------------------------+
;MM1 = | DV texel for p1 = 4dv + 10ddv | DV texel for p3 = 4dv + 18ddv |
; +---------------------------------------------------------------+
;This is because after the first four pixels are drawn on the screen, the
;loop repeats to draw the next four pixels. In order to get the next u, v
;texel coordinates, appropriate du, dv values need to be summed to u and v.
;The correct starting values of du and dv are:
;Pixel #0 = 4du + 6ddu ;Note: these have been mathematically proven.
;Pixel #1 = 4du + 10ddu
;Pixel #2 = 4du + 14ddu
;Pixel #3 = 4du + 18ddu
;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged.
MOVD MM0, du_init ;DU p1 = 0, p3 = du
MOVD MM1, dv_init ;DV p1 = 0, p3 = dv
PUNPCKLDQ MM0, MM0 ;DU p1 = du, p3 = du
PUNPCKLDQ MM1, MM1 ;DV p1 = dv, p3 = dv
MOVD MM2, ddu_init
PSLLD MM0, 2 ;DU p1 = 4du, p3 = 4du
MOVD MM3, ddv_init
PSLLD MM1, 2 ;DV p1 = 4dv, p3 = 4dv
PUNPCKLDQ MM2, MM2
PUNPCKLDQ MM3, MM3
PSLLD MM2, 1
PSLLD MM3, 1
PADDD MM0, MM2 ;DU p1 = 4du + 2ddu, p3 = 4du + 2ddu
PADDD MM1, MM3 ;DV p1 = 4dv + 2ddv, p3 = 4dv + 2ddv
PSLLD MM2, 2
PSLLD MM3, 2
PADDD MM0, MM2 ;DU p1 = 4du + 10ddu, p3 = 4du + 10ddu
MOVD MM2, ddu_init ;DDU p1 = 0, p3 = ddu
PADDD MM1, MM3 ;DV p1 = 4dv + 10ddv, p3 = 4dv + 10ddv
MOVD MM3, ddv_init ;DDV p1 = 0, p3 = ddv
PSLLD MM2, 3 ;DDU p1 = 0, p3 = 8ddu
PSLLD MM3, 3 ;DDV p1 = 0, p3 = 8ddv
PADDD MM0, MM2 ;DU p1 = 4du + 10ddu, p3 = 4du + 18ddu
PADDD MM1, MM3 ;DV p1 = 4dv + 10ddv, p3 = 4du + 18ddv
PSLLD MM2, 1 ;DDU p1 = 0, p3 = 16ddu
MOVQ DWORD PTR du, MM0
PUNPCKLDQ MM2, MM2 ;DDU p1 = 16ddu, p3 = 16ddu
MOVQ DWORD PTR dv, MM1
;Get the ddu ddv parameters in MMX(tm) technology form
;Note: ddu ddv texel values are stored in 10.22 fixed integer format.
;This sets up the ddu parameters for pixels 1 and 3 in MM0 register and
;ddv parameter in MM1 register. After setup, the registers will contain:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM0 = | DDU texel for p1 = 16ddu | DDU texel for p3 = 16ddu |
; +-----------------------------------------------------+
; +-----------------------------------------------------+
;MM1 = | DDV texel for p1 = 16ddv | DDV texel for p3 = 16ddv |
; +-----------------------------------------------------+
;This is because after the first four pixels are drawn on the screen, the
;loop repeats to draw the next four pixels. In order to get the next du, dv
;texel coordinates, appropriate ddu, ddv values need to be summed to du and dv.
;The correct values of ddu and ddv are:
;Pixel #0 = 16ddu ;Note: these have been mathematically proven.
;Pixel #1 = 16ddu
;Pixel #2 = 16ddu
;Pixel #3 = 16ddu
;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged.
PSLLD MM3, 1 ;DDV p1 = 0, p3 = 16ddv
MOVQ DWORD PTR ddu, MM2
PUNPCKLDQ MM3, MM3 ;DDV p1 = 16ddv, p3 = 16ddv
MOVQ DWORD PTR ddv, MM3
start_scan_line:
;First, the program converts the u and v texel coordinates
;from 10.22 format to 8.8 format. 10.22 format is used for
;decimal accuracy but only 16 of the 32 bits are actually used.
;Because the final format will fit in a 16 bit result, u and v
;values are converted from 4, 32 bit packed values
;to 4, 16 bit packed values that will fit in one MMX register. Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM0 = | U texel - p1 | U texel - p3 | V texel - p1 | V texel - p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;u_16bit = u_init >> 14;
;v_16bit = v_init >> 14;
MOVQ MM1, DWORD PTR u;
MOVQ MM0, DWORD PTR v;
PSRLD MM1, 14; ;Convert from 10.22 to 10.8
MOVQ MM2, DWORD PTR mask_32_to_15 ;Uses 15 instead of 16 because of signed saturation.
PSRLD MM0, 14; ;Convert from 10.22 to 10.8
PAND MM1, MM2 ;Convert from 10.8 to 7.8 integer format
PAND MM0, MM2 ;Convert from 10.8 to 7.8 integer format
MOVQ MM3, DWORD PTR mask_quad_1
PACKSSDW MM0, MM1 ;Pack the result into one register
;Calculation of the bx0, by0, bx1, by1 values for both pixels. Output:
; |-8 bit-|
; +-----------------------------------------------------------+
;MM2 = | |BX0 p1 | |BX0 p3 | |BY0 p1 | |BY0 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM3 = | |BX1 p1 | |BX1 p3 | |BY1 p1 | |BY1 p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;bx0 = u_16bit >> 8;
;by0 = v_16bit >> 8;
;bx1 = bx0 + 1;
;by1 = by0 + 1;
MOVQ MM1, DWORD PTR u ;Used for incrementing u for next 4 pix.
MOVQ MM2, MM0
MOVQ MM4, DWORD PTR du ;Used for incrementing u for next 4 pix.
PSRLW MM2, 8
PADDD MM1, MM4 ;Used for incrementing u for next 4 pix.
PADDUSB MM3, MM2
;Calculation of the rx0, ry0 values for both pixels. Final output:
; |-8 bit-|
; +-----------------------------------------------------------+
;MM0 = | |RX0 p1 | |RX0 p3 | |RY0 p1 | |RY0 p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;rx0 = u_16bit & 255;
;ry0 = v_16bit & 255;
PSLLW MM0, 8
MOVQ MM4, MM3
MOVQ MM6, DWORD PTR mask_quad_1
PUNPCKHWD MM4, MM2
PUNPCKLWD MM3, MM2
PMULLW MM4, MM4
PSRLW MM0, 8 ;MM0 = rx0 and ry0 param for pix 1, 3
;This section includes calculation of b00, b01, b10, b11. Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM4 = | b01 for p1 | b11 for p1 | b01 for p3 | b11 for p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM5 = | b00 for p1 | b10 for p1 | b00 for p3 | b10 for p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;b00 = random1((random1(bx0) + by0));
;b01 = random1((random1(bx0) + by1));
;b10 = random1((random1(bx1) + by0));
;b11 = random1((random1(bx1) + by1));
MOVQ MM2, MM3
MOVQ MM7, DWORD PTR du ;Used for incrementing du for next 4 pix
PUNPCKLDQ MM3, MM3
PUNPCKHDQ MM2, MM2
MOVQ MM5, MM4
MOVQ DWORD PTR u, MM1 ;Used for incrementing u for next 4 pix.
PUNPCKLWD MM4, MM4
PUNPCKHWD MM5, MM5
PADDW MM4, MM3
PADDW MM5, MM2
;This section calculates g_b00_0, b_b01_0, g_b10_0, g_b11_0 for pix 1 and 3.
;Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM2 = | g_b00_1 p3 | g_b01_1 p3 | g_b10_1 p3 | g_b11_1 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM3 = | g_b00_1 p1 | g_b01_1 p1 | g_b10_1 p1 | g_b11_1 p1 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM4 = | g_b00_0 p3 | g_b01_0 p3 | g_b10_0 p3 | g_b11_0 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM5 = | g_b00_0 p1 | g_b01_0 p1 | g_b10_0 p1 | g_b11_0 p1 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;g_b00_0 = (random2(b00) & 511) - 256;
;g_b01_0 = (random2(b01) & 511) - 256;
;g_b10_0 = (random2(b10) & 511) - 256;
;g_b11_0 = (random2(b11) & 511) - 256;
;g_b00_1 = (random2(b00 + 1) & 511) - 256;
;g_b01_1 = (random2(b01 + 1) & 511) - 256;
;g_b10_1 = (random2(b10 + 1) & 511) - 256;
;g_b11_1 = (random2(b11 + 1) & 511) - 256;
PMULLW MM4, MM4
PMULLW MM5, MM5
MOVQ MM2, MM6
MOVQ MM1, DWORD PTR ddu ;Used for incrementing du for next 4 pix
MOVQ MM3, MM6
PADDD MM7, MM1 ;Used for incrementing du for next 4 pix
PADDUSW MM2, MM4
PMULLW MM2, MM2
PADDUSW MM3, MM5
MOVQ MM1, DWORD PTR mask_quad_256
PMULLW MM3, MM3
MOVQ DWORD PTR du, MM7 ;Used for incrementing du for next 4 pix
PMULLW MM4, MM4
MOVQ MM7, DWORD PTR mask_quad_511
PMULLW MM5, MM5
PSRLW MM2, 2
PSRLW MM3, 2
PAND MM2, MM7
PSRLW MM4, 2
PAND MM3, MM7
PSRLW MM5, 2
PAND MM4, MM7
PAND MM5, MM7
PSUBW MM2, MM1 ;MM2 = g_b##_1 for pixel #3
PSUBW MM3, MM1 ;MM3 = g_b##_1 for pixel #1
PSUBW MM4, MM1 ;MM4 = g_b##_0 for pixel #3
PSUBW MM5, MM1 ;MM5 = g_b##_0 for pixel #1
;Take above data for g_b00_0, b_b01_0, g_b10_0, g_b11_0 for pix 1 and 3
;and rearrange the packed values in the MMX registers.
;Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM2 = | g_b00_0 p3 | g_b00_1 p3 | g_b01_0 p3 | g_b01_1 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM3 = | g_b00_0 p1 | g_b00_1 p1 | g_b01_0 p1 | g_b01_1 p1 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM6 = | g_b10_0 p3 | g_b10_1 p3 | g_b11_0 p3 | g_b11_1 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM7 = | g_b10_0 p1 | g_b10_1 p1 | g_b11_0 p1 | g_b11_1 p1 |
; +-----------------------------------------------------------+
MOVQ MM6, MM2
MOVQ MM7, MM3
PUNPCKHWD MM2, MM4 ;MM2 = g_b00_# and g_b01_# for pix #3
PUNPCKLWD MM6, MM4 ;MM6 = g_b10_# and g_b11_# for pix #3
PUNPCKHWD MM3, MM5 ;MM3 = g_b00_# and g_b01_# for pix #1
MOVQ MM4, MM0 ;Preparing for rx1 and ry1 calculation
PUNPCKLWD MM7, MM5 ;MM7 = g_b10_# and g_b11_# for pix #1
;Calculation of the rx1, ry1 values for both pixels. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM4 = | RX1 p1 | RX1 p3 | RY1 p1 | RY1 p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;rx1 = rx0 - 256;
;ry1 = ry0 - 256;
PSUBW MM4, MM1 ;MM4 = rx1 and ry1 parameters
;Setup for the calculation of u1 and u2 for pix #1. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM1 = | RX0 p1 | RY0 p1 | RX0 p1 | RY1 p1 |
; +-----------------------------------------------------------+
MOVQ MM5, MM0
MOVQ MM1, MM4
PSRLD MM5, 16
PSRAD MM1, 16
PSLLQ MM1, 32
PUNPCKHDQ MM1, MM5
PACKSSDW MM1, MM1
PACKSSDW MM5, MM5
PUNPCKLDQ MM1, MM5
;Calculation for U1 and U2 for pixel #1 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM3 = | U1 for pixel #1 | U2 for pixel #1 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;u1 = rx0 * g_b00_0 + ry0 * g_b00_1;
;u2 = rx0 * g_b01_0 + ry1 * g_b01_1;
PMADDWD MM3, MM1 ;MM3 = u1 and u2 for pixel #1
;Setup for the calculation of v1 and v2 for pix #1. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM5 = | RX1 p1 | RY0 p1 | RX1 p1 | RY1 p1 |
; +-----------------------------------------------------------+
MOVQ MM5, MM4
PSRAD MM5, 16
MOVQ MM1, MM0
PSRLD MM1, 16
PSLLQ MM1, 32
PUNPCKHDQ MM1, MM5
PACKSSDW MM1, MM1
PACKSSDW MM5, MM5
PUNPCKLDQ MM5, MM1
;Calculation for V1 and V2 for pixel #1 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM7 = | V1 for pixel #1 | V2 for pixel #1 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;v1 = rx1 * g_b00_0 + ry0 * g_b00_1;
;v2 = rx1 * g_b01_0 + ry1 * g_b01_1;
PMADDWD MM7, MM5 ;MM7 = v1 and v2 for pixel #1
;Setup for the calculation of u1 and u2 for pix #3. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM1 = | RX0 p3 | RY0 p3 | RX0 p3 | RY1 p3 |
; +-----------------------------------------------------------+
MOVQ MM5, MM0
PSLLD MM5, 16
PSRLD MM5, 16
MOVQ MM1, MM4
PSLLD MM1, 16
PSRAD MM1, 16
PUNPCKLDQ MM1, MM1
PUNPCKHDQ MM1, MM5
PACKSSDW MM1, MM1
PACKSSDW MM5, MM5
PUNPCKLDQ MM1, MM5
;Calculation for U1 and U2 for pixel #3 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM2 = | U1 for pixel #3 | U2 for pixel #3 |
; +-----------------------------------------------------+
PMADDWD MM2, MM1 ;MM2 = u1 and u2 for pixel #3
;Setup for the calculation of v1 and v2 for pix #3. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM4 = | RX1 p3 | RY0 p3 | RX1 p3 | RY1 p3 |
; +-----------------------------------------------------------+
PSLLD MM4, 16
PSRAD MM4, 16
MOVQ MM5, MM0
PSLLD MM5, 16
PSRAD MM5, 16
PUNPCKLDQ MM5, MM5
PUNPCKHDQ MM5, MM4
PACKSSDW MM5, MM5
PACKSSDW MM4, MM4
PUNPCKLDQ MM4, MM5
;Calculation for V1 and V2 for pixel #3 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM6 = | V1 for pixel #3 | V2 for pixel #3 |
; +-----------------------------------------------------+
PMADDWD MM6, MM4 ;MM6 = v1 and v2 for pixel #2
;Calculation for SX and SY for pixels #1 and #3, Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM1 = | SX p1 | SX p3 | SY p1 | SY p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;sx = (((rx0 * rx0) >> 1) * ((1536 - (rx0 << 2)))) >> 16;
;sy = (((ry0 * ry0) >> 1) * ((1536 - (ry0 << 2)))) >> 16;
MOVQ MM5, MM0
PMULLW MM5, MM5
MOVQ MM4, MM0
MOVQ MM1, DWORD PTR mask_quad_1536
PSLLW MM4, 2
PSUBD MM6, MM2 ;V1 - U1 and V2 - U2 for P3
PSUBD MM7, MM3 ;V1 - U1 and V2 - U2 for P1
PSUBW MM1, MM4
PSRLW MM5, 1
PMULHW MM1, MM5 ;MM1 = sx and sy param for pix 1, 3
;Calculation of A and B for pixel #1 and #3. Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM7 = | A for pixel #1 | B for pixel #1 |
; +-----------------------------------------------------+
; +-----------------------------------------------------+
;MM6 = | A for pixel #3 | B for pixel #3 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;a = u1 + sx * ((v1 - u1) >> 8);
;b = u2 + sx * ((v2 - u2) >> 8);
PSRAD MM7, 8
MOVQ MM0, DWORD PTR dv ;Used for incrementing v for next 4 pix
PSRAD MM6, 8
MOVQ MM4, MM1
MOVQ MM5, MM1
PSRLQ MM4, 16
PUNPCKLWD MM1, MM1
PUNPCKHDQ MM4, MM4
PMADDWD MM7, MM4
PSLLD MM5, 16
MOVQ MM4, DWORD PTR v ;Used for incrementing v for next 4 pix
PSRLD MM5, 16
PUNPCKHDQ MM5, MM5
PADDD MM4, MM0 ;Used for incrementing v for next 4 pix
PADDD MM7, MM3 ;MM7 = a and b parameter for pix #1
PMADDWD MM6, MM5
MOVQ MM3, DWORD PTR mask_double_65536
PSRLD MM1, 16
MOVQ DWORD PTR v, MM4 ;Used for incrementing v for next 4 pix
MOVQ MM5, DWORD PTR ddv ;Used for incrementing dv for next 4 pix
;Calculation of color indexes for pixel #1 and #3. Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM7 = | Color index for pixel #1 | Color index for pixel #3 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;color = (a + 65536 + sy * ((b - a) >> 8)) >> 9;
PADDD MM6, MM2 ;MM6 = a and b parameter for pix #3
PADDD MM0, MM5 ;Used for incrementing dv for next 4 pix
MOVQ MM4, DWORD PTR mask_quad_510
MOVQ MM2, MM6
MOVQ DWORD PTR dv, MM0 ;Used for incrementing dv for next 4 pix
PUNPCKLDQ MM6, MM7
MOVD MM0, ebx ;Move the last color written into MM2
PUNPCKHDQ MM2, MM7
PADDD MM3, MM2
PSUBD MM6, MM2
PSRAD MM6, 8
PMADDWD MM6, MM1
PADDD MM6, MM3
PSRLD MM6, 9 ;MM6 = color for pix #1 and #3
;Since the color values have been calculated for pixels 1 and 3,
;pixels 0 and 2 still need to be determined. Pixel 0 is calculated by
;(prev_pixel + pixel #1) / 2 and pixel 2 is calculated by (pixel #1 +
;pixel #3) / 2. Output:
; |--- 16 bit ----|
; +-----------------------------------------------------------------+
;MM3 = |Color p0 index | Color p1 index | Color p2 index | Color p3 index|
; +-----------------------------------------------------------------+
MOVD MM4, DWORD PTR mask_double_255
PACKSSDW MM6, MM6
MOVQ MM7, MM6
MOVQ MM3, MM6
PSRLD MM7, 16
PUNPCKLWD MM7, MM0
PADDW MM6, MM7
PSRLW MM6, 1
PUNPCKLWD MM3, MM6
;Now that MM3 contains the 4 memory indexes in packed format, we need
;to unpack them in order to get the precomputed color values from the 256
;element color array. Output:
; |--- 16 bit ---|
; +--------------------------------------------------------------+
;MM1 = | Color p3 | Color p2 | Color p1 | Color p0 |
; +--------------------------------------------------------------+
MOVQ MM2, MM3
MOVQ MM0, MM3
PSRLQ MM3, 48
MOVQ MM1, MM2
PAND MM0, MM4
PSRLD MM1, 16
MOVD EBX, MM0
PSRLQ MM2, 16
MOVD MM6, [ESI][EBX*2]
PSRLD MM2, 16
MOVD EAX, MM1
PAND MM2, MM4
MOVD MM0, [ESI][EAX*2]
MOVD EAX, MM2
PUNPCKLWD MM0, MM6
MOVD MM6, [ESI][EAX*2]
MOVD EAX, MM3
MOVD MM1, [ESI][EAX*2]
PUNPCKLWD MM1, MM6
PUNPCKLDQ MM1, MM0
ADD EDI, 8
;Write the 4 pixel colors to the backbuffer.
;Decrease the counter and loop back to draw four more pixels if necessary.
;The looping construct may look strange but it is done to allow for the
;calculation of the pixel colors at the end of the scan line.
MOVQ [EDI], MM1 ;Write out the 4 pix to video memory.
DEC ECX
JNZ start_scan_line
;Handle the end pixels of the scanline. This part draws between 0 and 3 end pixels.
;The 3 colors to possibly write are in register MM1.
start_end_pixels:
CMP EDX, 0
JZ end_scan_line
MOVQ MM2, MM1
ADD EDI, 8
MOVQ MM3, MM1
PSRLD MM2, 16
PSRLD MM3, 16
PUNPCKHWD MM3, MM1
PUNPCKLWD MM2, MM1
PUNPCKLDQ MM3, MM2
end_pixels:
MOVD EAX, MM3
MOV [EDI], AX
ADD EDI, 2
PSRLQ MM3, 16
DEC EDX
JNZ end_pixels
MOV prev_color, EBX ;EBX is the color index of pixel #3. Store it.
end_scan_line:
EMMS ;Clear out the MMX registers and set approp flags.
RET ;end of function
MMX_Noise ENDP
END
Appendix A - Possible Algorithm Modifications
Further work might be devoted to the following issues:
Appendix B - Marble Producing "C" Code
Additional code needed for the first marble texture.
//*****************************************************************************
//For generation of the marble textures from the noise function,
//comment out the line:
//"*(screen_buffer) = palette[color];"
//in the C_Noise() function and replace with the line:
//marble1(u_16bit, v_16bit, color, screen_buffer);
//Important! The functions marble1 and marble2 are designed only for
//16 bit 555 pixel format. Adaptation to the 565 and 24 bit true color is possible.
//*****************************************************************************
marble1(_int16 u_16bit, _int16 v_16bit,
unsigned char noise, _int16* screen_buffer)
{
float y;
unsigned long red, green, blue;
//Calculate the vertical component (vertical marble streaks).
//y range = 0.0 to 1.0
y = ((float)v_16bit) / 256.0 + (3.0 * ((float)noise)) / 256.0;
y = sin(y * 3.14159265);
y = (y + 1.0) * 0.5;
//Get weighted average of the horizontal color components.
//Color range = 0 to 255
green = ((long)((0.27 + 0.72 * y) * 256)) & 0xF8; //Conversion is only for 555 format.
red = ((long)((0.33 + 0.66 * y) * 256)) & 0xF8; //For those users with 565 color, make
blue = ((long)((0.60 + 0.39 * y) * 256)) & 0xF8; //changes as necessary.
//Conversion to 555 color format and write to the screen.
*(screen_buffer) = (red << 7) | (green << 2) | (blue >> 3);
}
Additional code needed for the second marble texture.
//Function used to generate the second sheet of marble.
//See directions for procedure marble1()
marble2(_int16 u_16bit, _int16 v_16bit,
unsigned char noise, _int16* screen_buffer)
{
float y1, y2;
unsigned long red1, green1, blue1;
unsigned long red2, green2, blue2;
unsigned long red, green, blue;
y1 = ((float)v_16bit) / 256.0 + (4.0 * ((float)noise)) / 256.0;
y1 = sin(y1 * 3.14159265);
y1 = (y1 + 1.0) * 0.5;
y2 = ((float)u_16bit) / 256.0 + (9.0 * ((float)noise)) / 256.0;
y2 = sin(y2 * 2.0797343366);
y2 = (y2 + 1.0) * 0.5;
green1 = (long)((0.25 + 0.75 * y1) * 128.0);
red1 = (long)((0.35 + 0.65 * y1) * 128.0);
blue1 = (long)((0.32 + 0.68 * y1) * 128.0);
green2 = (long)((0.25 + 0.75 * y2) * 128.0);
red2 = (long)((0.28 + 0.72 * y2) * 128.0);
blue2 = (long)((0.35 + 0.65 * y2) * 128.0);
red = (red1 + red2) & 0xF8; //Conversion is only for 555 format.
green = (green1 + green2) & 0xF8; //For those users with 565 color, make app
blue = (blue1 + blue2) & 0xF8; //changes.
*(screen_buffer) = (red << 7) | (green << 2) | (blue >> 3);
}
Appendix C - Texture Creation
How to create textures like Figure 1.x
To create new sample textures as seen in Figure 1.x, there are two main things
to be done. One is setting the zoom detail of the texture and the other
is setting up the palette correctly. The sample program provided with this
application note will be required to do this.
The test program reads in a palette from the file "palette.pal". For those wishing to create their own palette to use for the texture routine, follow these steps:
Here's the black & white palette used for figure 1.3, the star scene.
Appendix E - Algorithm Testing
The code was tested using:
Basic Functionality: